Multithreaded: Summation of a Vector

My goal is to sum up all elements of a vector. I used in the last post a single thread. In this post, I use multiple threads and, therefore, the full power of my PC. The addition will be done on a shared variable. What, at first glance, seems like a good idea is a very naive strategy. The synchronization overhead of the summation variable is higher than the performance benefit of my four or two cores.

The strategy

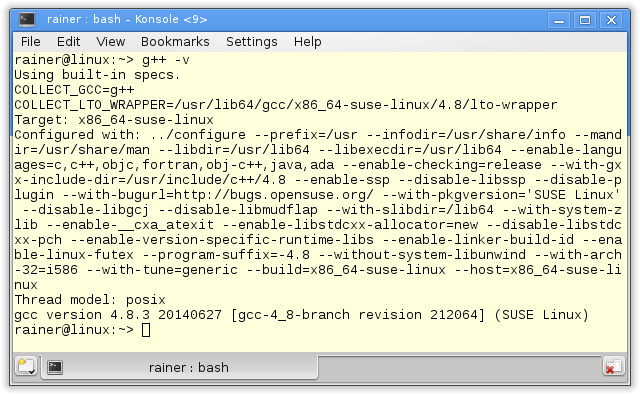
Following my last post, I sum up 100 000 000 million random numbers between 1 and 10. To be sure that my calculation is right I reduce the randomness. So I use no seed, and I get each time the same random numbers on my two architectures each. Therefore it’s easy to verify my total result. Both calculations will run on my 4-CPU Linux and my 2-CPU Windows PC, as ever, with maximum and without optimization. On Windows, I was very puzzled.

What are the exciting questions?

How differs locks and atomics work?
What’s the difference between the single threaded and the multithreading execution of std::accumulate?

Protection of the shared variable with the std::lock_guard

The simplest way to protect a shared variable is to wrap a mutex in a lock.

// synchronizationWithLock.cpp

#include <chrono>
#include <iostream>
#include <mutex>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

std::mutex myMutex;

void sumUp(unsigned long long& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
        std::lock_guard<std::mutex> myLock(myMutex);
        sum+= val[it];
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  unsigned long long sum= 0;
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

The program is easy to explain. The function sumUp (lines 20 – 25) is each thread’s work package. This work package consists of the summation variable sum and the std::vector val, both getting by reference. beg and end limit the range on which the summation takes place. As mentioned, I use a std::lock_guard (line 22) to protect the shared variable. Each thread line 41 – 44 does a quarter of the work.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Here are the numbers of the program.

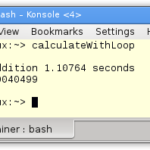
Without optimization

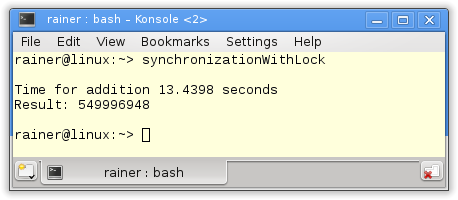
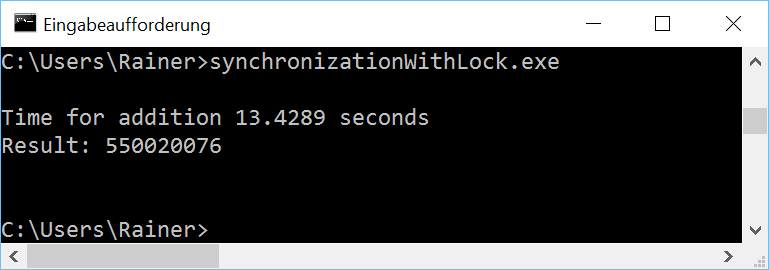
Maximum optimization

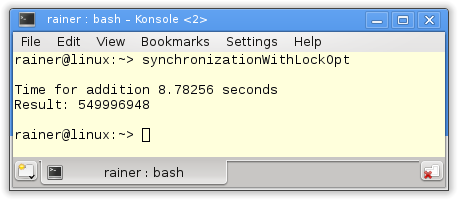
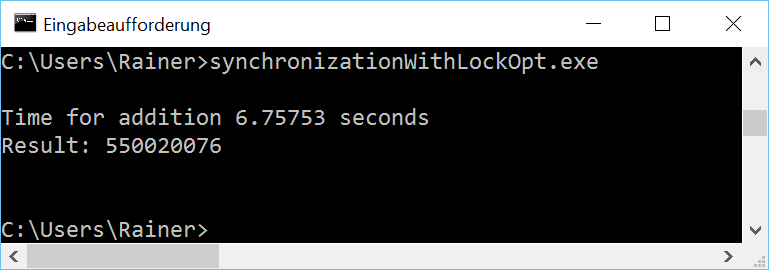
The bottleneck of the program is the shared variable, which is expensively protected by a std::lock_guard. Therefore the obvious solution is to replace the heavyweight lock with a lightweight atomic.

Addition with an atomic

The variable sum is atomic. So I can skip the std::lock_guard in the function sumUp (lines 18 – 22). That was all.

// synchronizationWithAtomic.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
        sum+= val[it];
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum(0);
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Without optimization

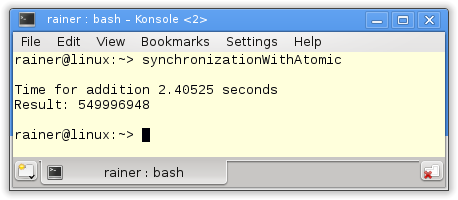
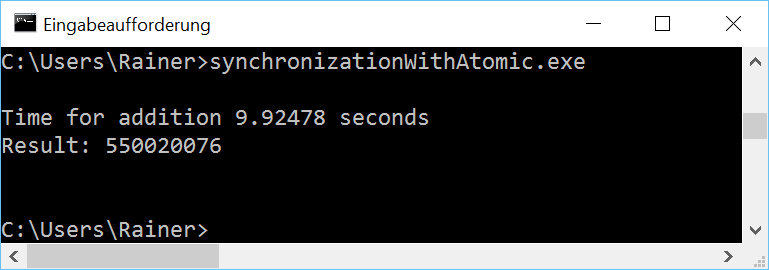
Maximum optimization

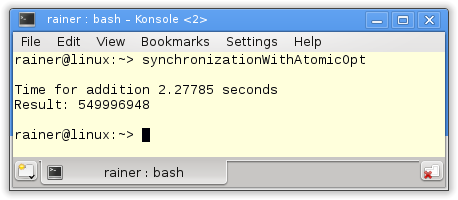
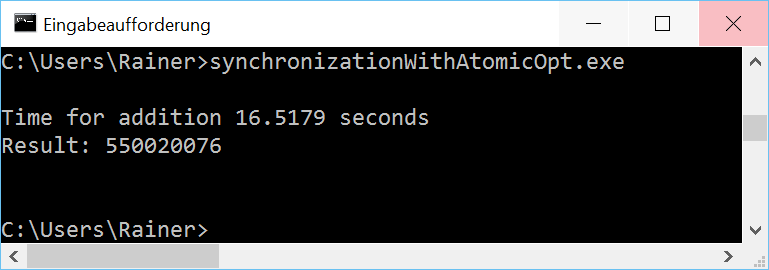
A strange phenomenon

If you study the numbers carefully, you will notice a strange phenomenon on Windows. The maximum optimized program is slower than the non-optimized one. That observation will also hold for the next two variations. This puzzled me. I executed the program in addition to a virtualized Windows 8 PC with only one core. Here the optimized version was faster. Something strange is going on with my Windows 10 PC and atomics.

Besides +=, there is a further way to calculate the sum of an atomic with fetch_add. Let’s try it out. The numbers should be similar.

Addition with fetch_add

The change in the source code is minimal. I have only to touch line 20.

// synchronizationWithFetchAdd.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
		sum.fetch_add(val[it]);
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum(0);
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Without optimization

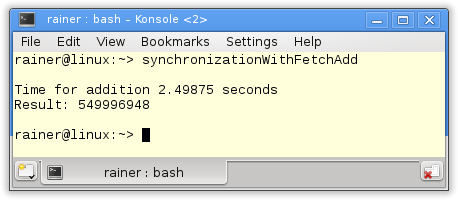
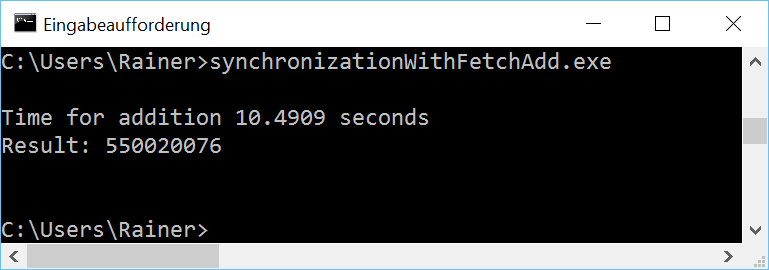
Maximum optimization

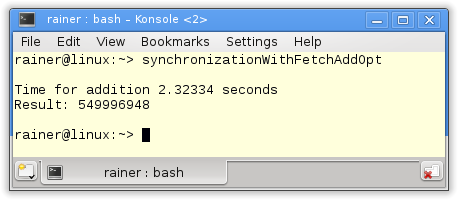
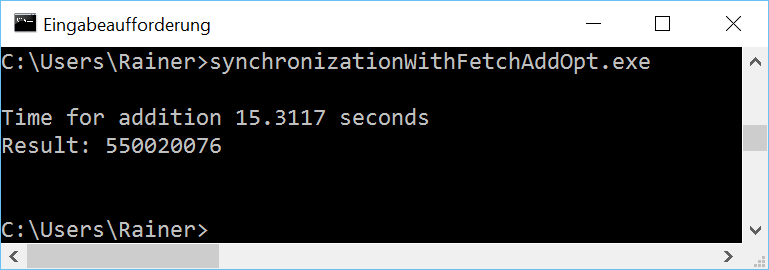
Strictly speaking, is the fetch_add variation no improvement to the += variation but the contrary? The += variation is more intuitive. But wait, there is a small difference.

In addition, with fetch_add and relaxed semantic

The default behavior for atomics is sequential consistency. This statement is true for adding and assigning an atomic and, of course, for the fetch_add variant. But we can do better. Let’s adjust the memory model with the fetch variations. That’s the final step in my optimization. You see it in line 20.

// synchronizationWithFetchAddRelaxed.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto it= beg; it < end; ++it){
		sum.fetch_add(val[it],std::memory_order_relaxed);
    }
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum(0);
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

The question is. Why is it ok to use the relaxed-semantics in line 20? Relaxed-semantics will not guarantee that one thread sees the operation in another in the same order. But this is not necessary. Necessary is only that each addition is atomically performed.

Does the optimization pay off?

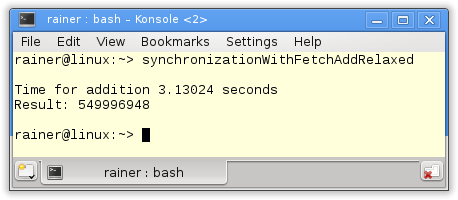
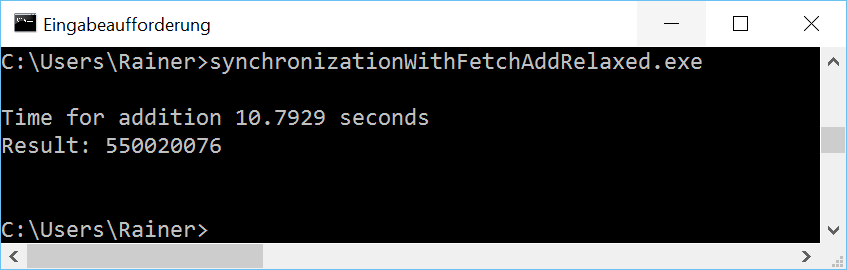
Without optimization

Maximum optimization

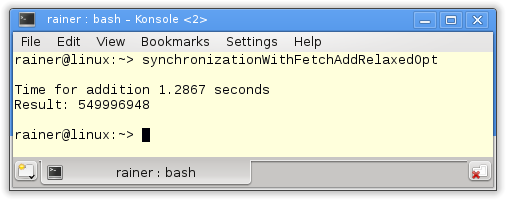
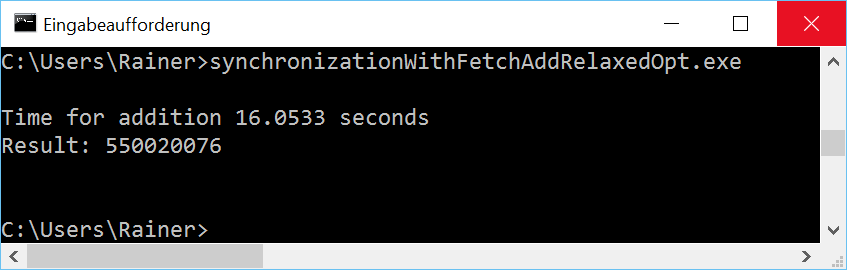
As expected, for Linux and GCC is, the fetch_add variant with relaxed-semantic the fastest one. I’m still puzzled with Windows.

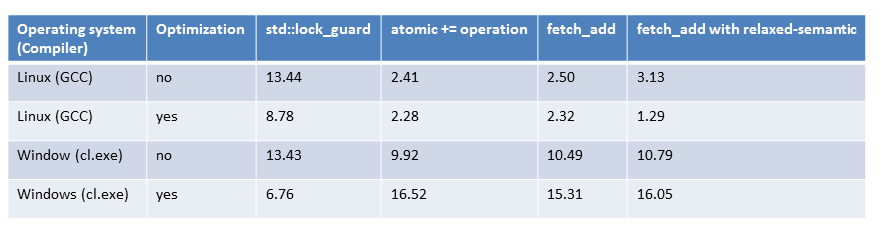
In the end, all numbers are together in a table.

The overview

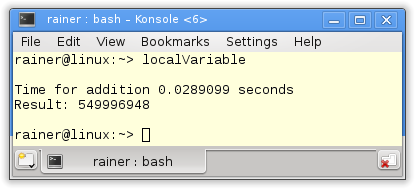
Although I have successively optimized the access to the shared variable and improved the performance accordingly, the results are not very promising. The addition in the single threaded case with std::accumulate is far faster. To say it precisely 40 times.

What’s next?

I will combine in the next post the best of the two worlds. I combine the non-synchronized summation in one thread with the power of many threads. Let’s see if I beat the performance of the single thread variant of std::accumulate.

Post Views: 5,027

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS