Multithreaded: Summation with Minimal Synchronization

9 September 2016
Contents[Show]

Until now, I've used two strategies to summate a std::vector. First, I did the whole math in one thread (Single Threaded: Summation of a vector); second multiple threads shared the same variable for the result (Multithreaded: Summation of a vector). In particular, the second strategy was extremely naive. In this post, I will apply my knowledge of both posts. My goal is that the thread will perform their summation as independently from each other as possible and therefore reduce the synchronization overhead. 

 

To let the threads work independently and therefore minimize the synchronization, I have a few ideas in my mind. Local variables, thread-local data but also tasks should work. Now I'm curious.

 

Rainer D 6 P2 540x540Modernes C++ Mentoring

Be part of my mentoring programs:

 

 

 

 

Do you want to stay informed about my mentoring programs: Subscribe via E-Mail.

My strategy

My strategy keeps the same. As in my last post, I use my desktop PC with four cores and GCC and my laptop with two cores and cl.exe. I provide the results without and with maximum optimization. For the details, look here: Thread-safe initialization of a singleton. 

Local variables

Since each thread has a local summation variable, it can do its job without synchronization. It's only necessary to sum up the local summation variables. Adding the local results is a critical section that must be protected. This can be done in various ways. A quick remark before. Since only four addition takes place, it doesn't matter so much from a performance perspective which synchronization I will use. But instead of my remark, I will use a std::lock_guard and an atomic with sequential consistency and relaxed semantics.

std::lock_guard

 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
 
// localVariable.cpp

#include <mutex>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

std::mutex myMutex;

void sumUp(unsigned long long& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    unsigned long long tmpSum{};
    for (auto i= beg; i < end; ++i){
        tmpSum += val[i];
    }
    std::lock_guard<std::mutex> lockGuard(myMutex);
    sum+= tmpSum;
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  unsigned long long sum{}; 
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

 

Lines 25 and 26 are critical lines. Here the local summation results tmpSum will be added to the global sum. What is the spot at which the examples with the local variables will vary?

Without optimization

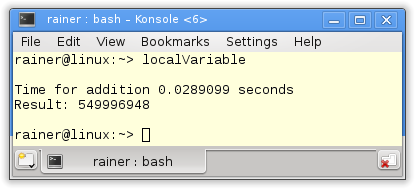
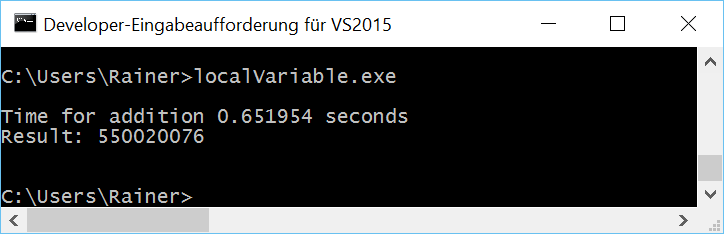
localVariablelocalVariablewin

Maximum optimization

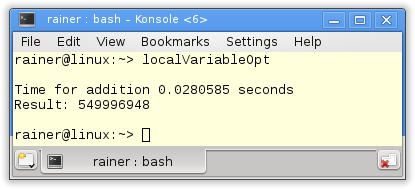
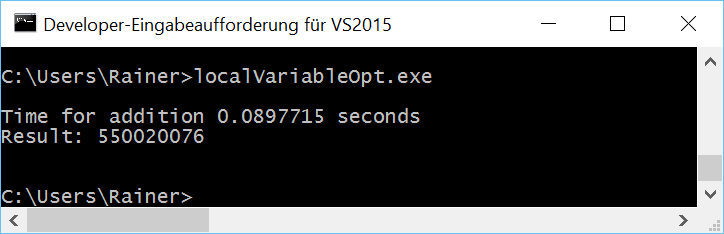
localVariableOptlocalVariableOptwin

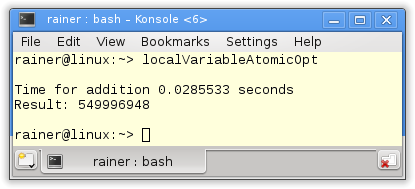
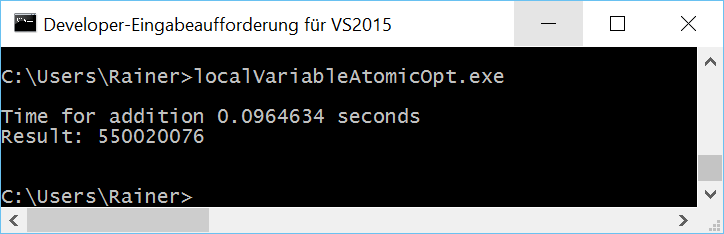
Atomic operations with sequential consistency

My first optimization is it to replace the by a std::lock_guard protected global summation sum variable with an atomic.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
 
// localVariableAtomic.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    unsigned int long long tmpSum{};
    for (auto i= beg; i < end; ++i){
	    tmpSum += val[i];
    }
    sum+= tmpSum;
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum{}; 
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

Without optimization

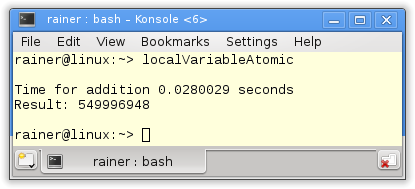
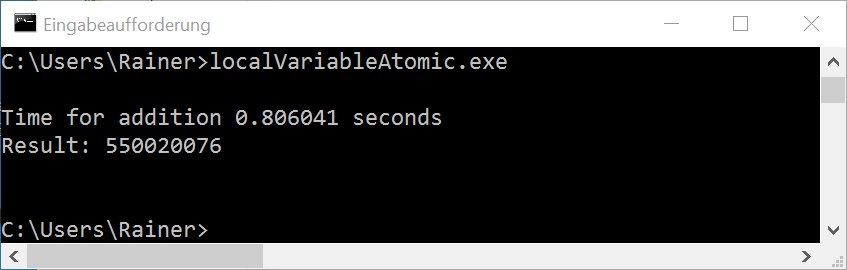
localVariableAtomiclocalVariableAtomicwin

Maximum optimization

 localVariableAtomicOptlocalVariableAtomicOptwin

Atomic operations with relaxed semantic

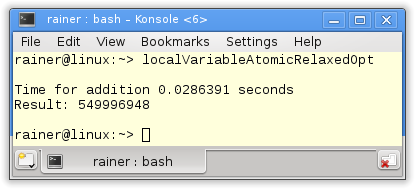
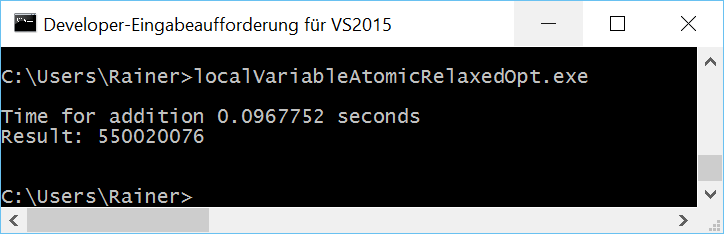
We can do better. Instead of the default memory model of sequential consistency, I use relaxed semantics. That's well-defined because it doesn't matter in which order the additions in line 23 take place.

 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
 
// localVariableAtomicRelaxed.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    unsigned int long long tmpSum{};
    for (auto i= beg; i < end; ++i){
	    tmpSum += val[i];
    }
    sum.fetch_add(tmpSum,std::memory_order_relaxed);
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum{}; 
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
 
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

 

Without optimization

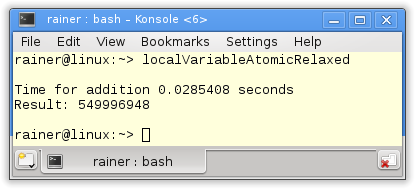
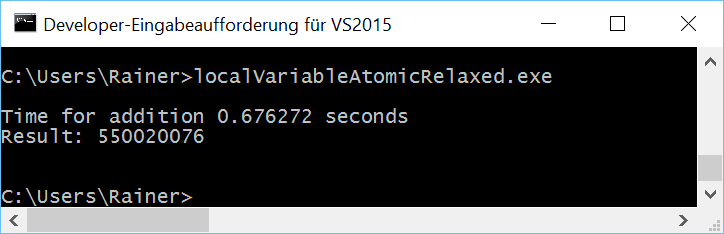
localVariableAtomicRelaxedlocalVariableAtomicRelaxedwin

Maximum optimization

localVariableAtomicRelaxedOptlocalVariableAtomicRelaxedOptwin

The following strategy is similar. But now I use thread local data.

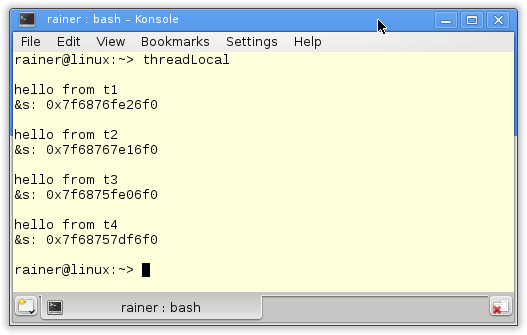
Thread local data

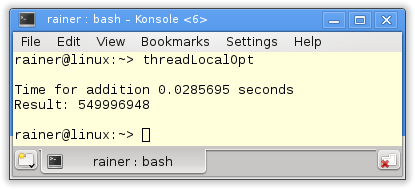
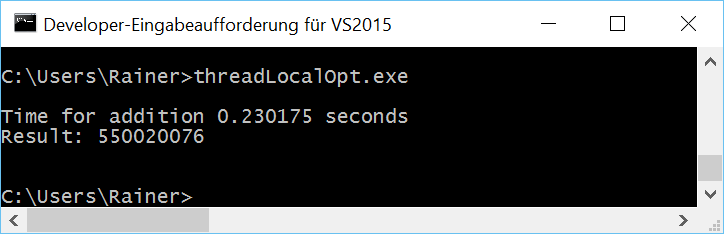
Thread local data is data that each thread exclusively owns. They will be created when needed. Therefore, thread local data perfectly fit the local summation variable tmpSum.

 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
 
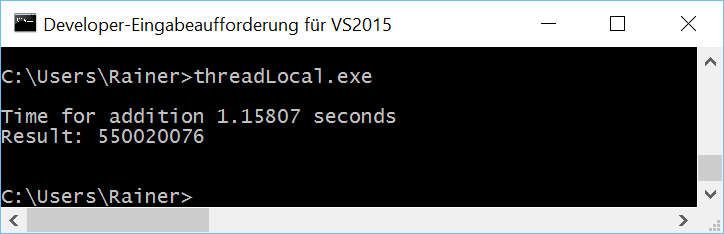
// threadLocal.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

thread_local unsigned long long tmpSum= 0;

void sumUp(std::atomic<unsigned long long>& sum, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
    for (auto i= beg; i < end; ++i){
        tmpSum += val[i];
    }
    sum.fetch_add(tmpSum,std::memory_order_relaxed);
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::atomic<unsigned long long> sum{}; 
  auto start = std::chrono::system_clock::now();
  
  std::thread t1(sumUp,std::ref(sum),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::ref(sum),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::ref(sum),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::ref(sum),std::ref(randValues),thiBound,fouBound);   
  
  t1.join();
  t2.join();
  t3.join();
  t4.join();
  
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;

  std::cout << std::endl;

}

 

I declare in line 18 the thread-local variable tmpSum and use it for the addition in lines 22 and 24. The small difference between the thread-local variable and the local variable in the previous programs is that the thread-local variable's lifetime is bound to its thread's lifetime. The lifetime of the local variable depends on its scope.

Without optimization

threadLocalthreadLocalwin

Maximum optimization

threadLocalOptthreadLocalOptwin

The question is. Is it possible to calculate the sum in a fast way without synchronization? Yes.

Tasks

With task, we can do the whole job without synchronization. Each summation is performed in a separate thread and the final summation is in a single thread. Here are the details of tasks. I will use promise and future in the following program.

 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
 
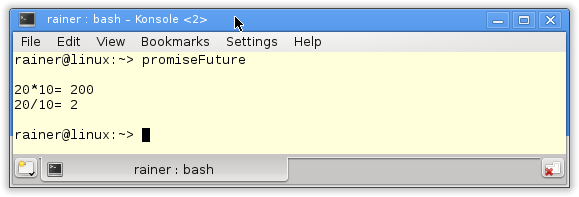
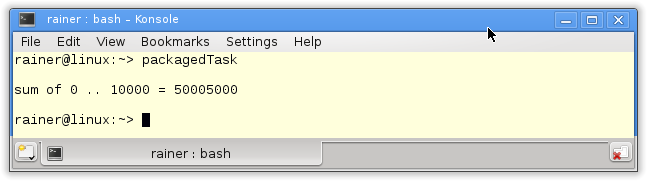
// tasks.cpp

#include <chrono>
#include <future>
#include <iostream>
#include <random>
#include <thread>
#include <utility>
#include <vector>

constexpr long long size= 100000000;   

constexpr long long firBound=  25000000;
constexpr long long secBound=  50000000;
constexpr long long thiBound=  75000000;
constexpr long long fouBound= 100000000;

void sumUp(std::promise<unsigned long long>&& prom, const std::vector<int>& val, unsigned long long beg, unsigned long long end){
	unsigned long long sum={};
	for (auto i= beg; i < end; ++i){
	    sum += val[i];
    }
    prom.set_value(sum);
}

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  std::mt19937 engine;
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  std::promise<unsigned long long> prom1;
  std::promise<unsigned long long> prom2;
  std::promise<unsigned long long> prom3;
  std::promise<unsigned long long> prom4;
  
  auto fut1= prom1.get_future();
  auto fut2= prom2.get_future();
  auto fut3= prom3.get_future();
  auto fut4= prom4.get_future();
  
  
  auto start = std::chrono::system_clock::now();

  std::thread t1(sumUp,std::move(prom1),std::ref(randValues),0,firBound);
  std::thread t2(sumUp,std::move(prom2),std::ref(randValues),firBound,secBound);
  std::thread t3(sumUp,std::move(prom3),std::ref(randValues),secBound,thiBound);
  std::thread t4(sumUp,std::move(prom4),std::ref(randValues),thiBound,fouBound);
  
  auto sum= fut1.get() + fut2.get() + fut3.get() + fut4.get();
 
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << sum << std::endl;
  
  t1.join();
  t2.join();
  t3.join();
  t4.join();

  std::cout << std::endl;

}

 

I define in lines 37 - 45 the four promises and create from them the associated futures. Each promise is moved in lines 50 - 52 in a separate thread. A promise can only be moved; therefore, I use std::move. The work package of the thread is the function sumUp (lines 18 - 24). sumUp takes as the first argument a promise by rvalue reference. The futures ask in line 55 for the results. The get call is blocking. 

Without optimization

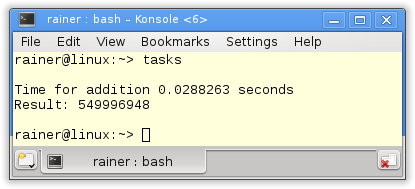
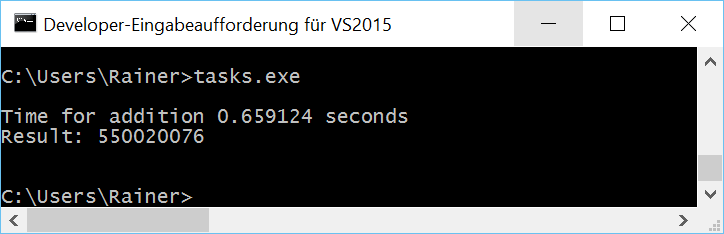
taskstaskswin

Maximum optimization

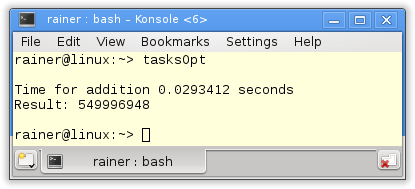
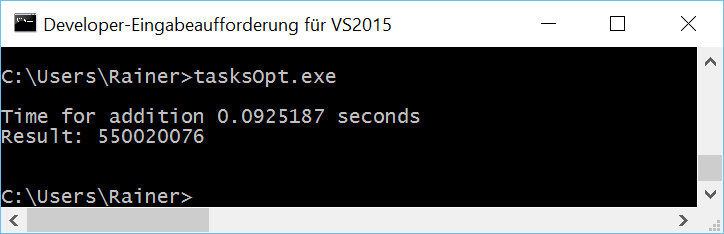
tasksOpttasksOptwin

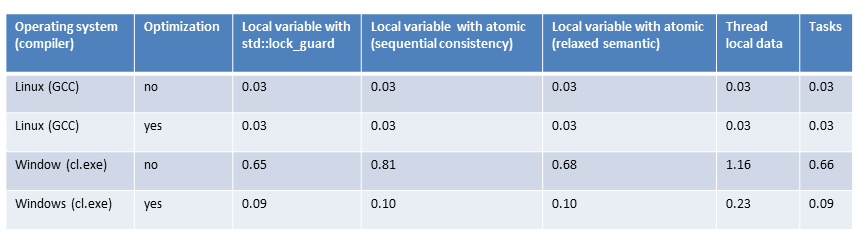
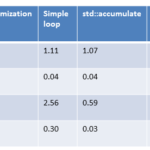
All numbers in the overview

The overview

As previously mentioned, the numbers are quite similar for Linux. That's no surprise because I always use the same strategy: Calculate the partial sum locally without synchronization and add the local sums. The addition of the partial sums has to be synchronized. What astonished me was that maximum optimization makes no significant difference. 

On Windows, the story is different. First, it makes a big difference if I compile the program with maximum or without optimization; second, Windows is much slower than Linux. I'm unsure if that is since Windows has only two cores but Linux 4.

 MultipleThreadsEng

What's next?

I will reason in the next post about the numbers for summing up a vector and the results that can be derived from it.

 

 

 

 

 

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Animus24, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Kris Kafka, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Matthieu Bolt, Stephen Kelley, Kyle Dean, Tusar Palauri, Dmitry Farberov, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, and Rob North.

 

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, and Slavko Radman.

 

 

My special thanks to Embarcadero CBUIDER STUDIO FINAL ICONS 1024 Small

 

My special thanks to PVS-Studio PVC Logo

 

My special thanks to Tipi.build tipi.build logo

 

My special thanks to Take Up Code TakeUpCode 450 60

 

Seminars

I'm happy to give online seminars or face-to-face seminars worldwide. Please call me if you have any questions.

Bookable (Online)

German

Standard Seminars (English/German)

Here is a compilation of my standard seminars. These seminars are only meant to give you a first orientation.

  • C++ - The Core Language
  • C++ - The Standard Library
  • C++ - Compact
  • C++11 and C++14
  • Concurrency with Modern C++
  • Design Pattern and Architectural Pattern with C++
  • Embedded Programming with Modern C++
  • Generic Programming (Templates) with C++

New

  • Clean Code with Modern C++
  • C++20

Contact Me

Modernes C++,

RainerGrimmDunkelBlauSmall

Tags: Atomics, Sequential Consistency, Relaxed Semantics, thread_local, Tasks, Performance

Comments   

0 #1 Music Albums 2016-11-13 02:40
Usually I don't read post on blogs, but I would
like to say that this write-up very forced me to take a look at and do so!

Your writing style has been surprised me. Thank you,
quite great article.
Quote
0 #2 Tracks 320 kbps 2016-11-17 11:28
Hi, I do think this is a great web site.
I stumbledupon it ;) I will come back once again since i
have book marked it. Money and freedom is the best way to change, may you be rich and continue to guide other people.
Quote
0 #3 Tracks 320 kbps 2016-11-28 03:55
Wonderful article! We are linking to this great article on our website.
Keep up the good writing.
Quote
0 #4 Tracks 320 kbps 2016-12-17 05:09
Excellent pieces. Keep posting such kind of info on your
page. Im really impressed by your site.
Hey there, You have done an excellent job. I will definitely digg it
and individually recommend to my friends. I am sure they will be benefited from this site.
Quote

Stay Informed about my Mentoring

 

Mentoring

English Books

Course: Modern C++ Concurrency in Practice

Course: C++ Standard Library including C++14 & C++17

Course: Embedded Programming with Modern C++

Course: Generic Programming (Templates)

Course: C++ Fundamentals for Professionals

Course: The All-in-One Guide to C++20

Course: Master Software Design Patterns and Architecture in C++

More Profiles

Contact

Subscribe to the newsletter (+ pdf bundle)

Categories

All tags

Blog archive

Source Code

Most Popular Posts

Visitors

Today 1469

Yesterday 6503

Week 27726

Month 7972

All 12086181

Currently are 198 guests and no members online

Kubik-Rubik Joomla! Extensions

Latest comments