Single Threaded: Summation of a Vector

What is the fastest way to add the elements of a std::vector? This a question that I will pursue in the following posts. I use the single-threaded addition as the reference number. In further posts, I discuss atomics, locks, and thread-local data.

My strategy

My plan is to fill a std::vector with one hundred million arbitrary numbers between 1 and 10. I apply the uniform distribution to get the numbers. The task is to calculate the sum of all values.

I usually use my Linux desktop and Windows laptop to get the numbers. The Linux PC has four, and my Windows PC has two cores. Here are details of my compilers: Thread-safe initialization of a singleton. I will measure the performance with and without maximum optimization.

A simple loop

The obvious strategy is to add the numbers in a range-based for loop.

// calculateWithLoop.cpp

#include <chrono>
#include <iostream>
#include <random>
#include <vector>

constexpr long long size= 100000000;

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  // random values
  std::random_device seed;
  std::mt19937 engine(seed());
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  auto start = std::chrono::system_clock::now();
  
  unsigned long long add= {};
  for (auto n: randValues) add+= n;
 
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << add << std::endl;

  std::cout << std::endl;

}

The calculation takes place in line 26. How fast are my computers?

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Without optimization

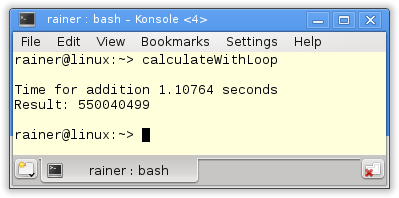
Maximum optimization

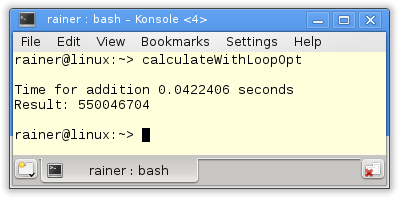
You should not use explicit loops. A rule which, in particular, holds for Windows. That’s simple therefore, I have to look in the Standard Template Library (STL).

The STL with std::accumulate

std::accumulate is the standard way to calculate the sum.

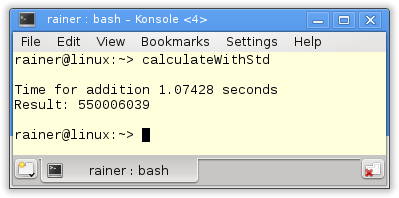
// calculateWithStd.cpp

#include <algorithm>
#include <chrono>
#include <iostream>
#include <numeric>
#include <random>
#include <vector>

constexpr long long size= 100000000;

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  // random values
  std::random_device seed;
  std::mt19937 engine(seed());
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
 
  auto start = std::chrono::system_clock::now();
  
  unsigned long long add= std::accumulate(randValues.begin(),randValues.end(),0);
 
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << add << std::endl;

  std::cout << std::endl;

}

The key lines are line 27. The performance of std::acummulate corresponds to the performance of the range-based for loop. But not for Windows.

Without optimization

Maximum optimization

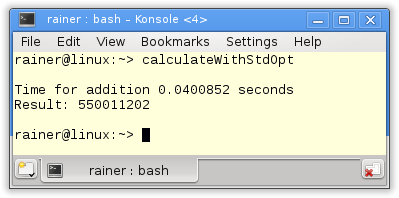
That was all. I have my numbers to compare the single-threaded with the multithreading program. Really? I’m very curious about protecting the summation with a lock or using an atomic. So we get the overhead of protection.

Protection by a lock

If I protect the access to the summation variable with a lock, I get the answers to my two questions.

How expensive is the synchronization of a lock?
How fast can a lock be if no concurrent access to a variable takes place?

Of course, I can rephrase point 2. If more the one thread accesses the shared variable, the access time decreases.

// calculateWithLock.cpp

#include <chrono>
#include <iostream>
#include <mutex>
#include <numeric>
#include <random>
#include <vector>

constexpr long long size= 100000000;

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  // random values
  std::random_device seed;
  std::mt19937 engine(seed());
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));

  std::mutex myMutex;
 
  unsigned long long int add= 0;
  auto start = std::chrono::system_clock::now();
  
  for (auto i: randValues){
      std::lock_guard<std::mutex> myLockGuard(myMutex);
      add+= i;
  }
 
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << add << std::endl;
    
  std::cout << std::endl;

}

That’s the result I assumed. The access on the protected variable add is slower.

Without optimization

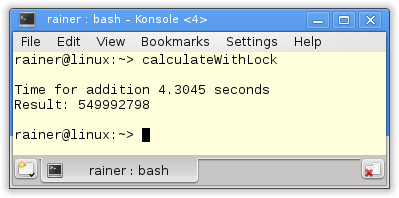
Maximum optimization

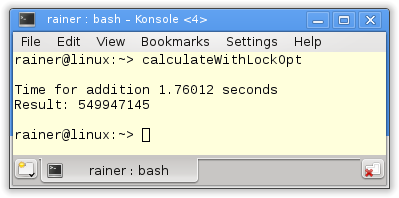
The non-optimized version with the lock is 4 – 12 times slower than the maximum optimized. The maximum optimized about 10 – 40 times slower than std::accumulate.

Finally atomics.

Protection by an atomic

The same question for locks holds also for atomics.

How expensive is the synchronization of a lock?
How fast can a lock be if no concurrent access to a variable takes place?

But there is an additional question. What is the performance difference between an atomic and a lock?

// calculateWithAtomic.cpp

#include <atomic>
#include <chrono>
#include <iostream>
#include <numeric>
#include <random>
#include <vector>

constexpr long long size= 100000000;

int main(){

  std::cout << std::endl;

  std::vector<int> randValues;
  randValues.reserve(size);

  // random values
  std::random_device seed;
  std::mt19937 engine(seed());
  std::uniform_int_distribution<> uniformDist(1,10);
  for ( long long i=0 ; i< size ; ++i) randValues.push_back(uniformDist(engine));
  
  std::atomic<unsigned long long> add={};
  std::cout << std::boolalpha << "add.is_lock_free(): " << add.is_lock_free() << std::endl;
  std::cout << std::endl;
 
  auto start = std::chrono::system_clock::now();
  
  for (auto i: randValues) add+= i;
 
  std::chrono::duration<double> dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << add << std::endl;
    
  std::cout << std::endl;
  
  add=0;
  start = std::chrono::system_clock::now();
  
  for (auto i: randValues) add.fetch_add(i,std::memory_order_relaxed);
  
  dur= std::chrono::system_clock::now() - start;
  std::cout << "Time for addition " << dur.count() << " seconds" << std::endl;
  std::cout << "Result: " << add << std::endl;
    
  std::cout << std::endl;

}

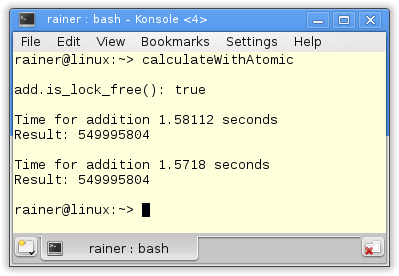
The program is special. First, I ask in line 26 if the atomic has a lock. That is crucial because otherwise, there is no difference between using locks and atomics. On all mainstream platforms, I knew atomics use no lock. Second I calculate the sum in two ways. I use in line 31 the += operator; in line 42, the method fetch_add. Both variants have, in the single-threaded case, a comparable performance, but I can explicitly specify in the case of fetch_add the memory model. More about that point in the next post.

But now the numbers.

Without optimization

Maximum optimization

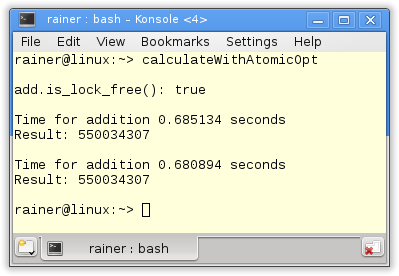
In the case of Linux, the atomics are 1.5 times slower, and in the case of windows eight times slower than the std::accumulate algorithm. That changes even more in the case of optimization. Now Linux is 15 times; Windows is 50 times faster.

I want to stress two points.

Atomics are 2 – 3 times faster on Linux and Windows than locks.
Linux is, in particular, for atomics two times faster than Windows.

All numbers compact

How lost the orientation because of the number? Here is the overview in seconds.

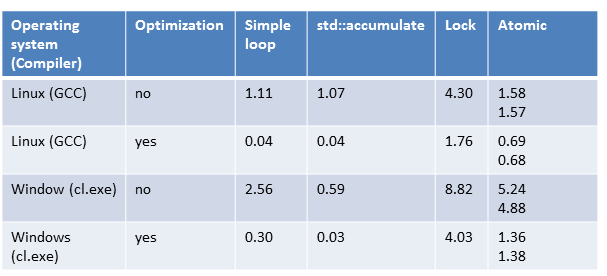
What’s next?

Single-threaded becomes multithreaded in the next post. In the first step, the summation variable add becomes a shared variable used by four threads. In the second step, add will be atomic.

Post Views: 5,988

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS