C++ Core Guidelines: Ordering of User-Defined Types

My post for today is just loosely coupled to the rules of the C++ core guidelines because they do provide not much content. Inspired by the guidelines, today’s post concerns a generic isSmaller function.

Here are the rules for today. They are about the specialization of templates.

The specialization of function templates is also one of my topics for today.

Comparing two Accounts: The First

Let me start simply. I have a class Account. I want to know if an account is smaller than another account. Smaller means, in this case, that the balance is lower.

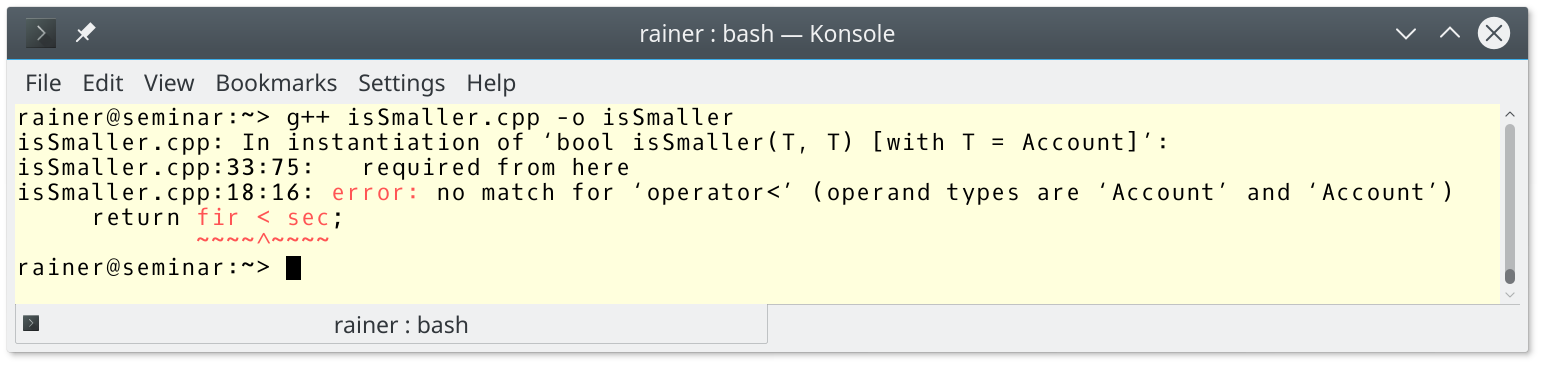
// isSmaller.cpp

#include <iostream>

class Account{
public:
  Account() = default;
  Account(double b): balance(b){}
  double getBalance() const {
    return balance;
  }
private:
  double balance{0.0};
};

template<typename T>                     // (1)
bool isSmaller(T fir, T sec){
    return fir < sec;
}

int main(){

    std::cout << std::boolalpha << std::endl;

    double firDoub{};
    double secDoub{2014.0};

    std::cout << "isSmaller(firDoub, secDoub): " 
              << isSmaller(firDoub, secDoub) << std::endl;

    Account firAcc{};
    Account secAcc{2014.0};

    std::cout << "isSmaller(firAcc, secAcc): " 
              << isSmaller(firAcc, secAcc) << std::endl;
    
    std::cout << std::endl;

}

To simplify my job, I wrote a generic isSmaller function (1) for comparing two values. As you presumably expected, I can not compare accounts because its operator< is not overloaded.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Before I variously solve this issue, I want to make a short detour to SemiRegular and Regular types. This is for one reason the original definition of Regular from Alexander Stepanov and the definition as a concept in C++20 differs in one critical point: ordering.

SemiRegular and Regular Types

Rule T.67: Use specialization to provide alternative implementations for irregular types talks about irregular types. The informal term irregular types stand for either SemiRegular or Regular. To remind you. Here is the definition of SemiRegular and Regular types.

Regular

DefaultConstructible
CopyConstructible, CopyAssignable
MoveConstructible, MoveAssignable
Destructible
Swappable
EqualityComparable

SemiRegular

SemiRegular – EqualityComparable

If you want more details about Regular and SemiRegular, read my post C++ Core Guidelines: Regular and SemiRegular Types. The account is a SemiRegular but not a Regular type.

// accountSemiRegular.cpp

#include <experimental/type_traits>
#include <iostream>

class Account{
public:
  Account() = default;
  Account(double b): balance(b){}
  double getAccount() const {
    return balance;
  }
private:
  double balance{0.0};
};

template<typename T>
using equal_comparable_t = decltype(std::declval<T&>() == std::declval<T&>());

template<typename T>
struct isEqualityComparable: 
       std::experimental::is_detected<equal_comparable_t, T>
       {};

template<typename T>
struct isSemiRegular: std::integral_constant<bool,
                                      std::is_default_constructible<T>::value &&
                                      std::is_copy_constructible<T>::value &&
                                      std::is_copy_assignable<T>::value &&
                                      std::is_move_constructible<T>::value &&
                                      std::is_move_assignable<T>::value &&
                                      std::is_destructible<T>::value &&
                                      std::is_swappable<T>::value >{};

template<typename T>
struct isRegular: std::integral_constant<bool, 
                                         isSemiRegular<T>::value &&
                                         isEqualityComparable<T>::value >{};

int main(){

    std::cout << std::boolalpha << std::endl;

    std::cout << "isSemiRegular<Account>::value: " << isSemiRegular<Account>::value << std::endl;
    std::cout << "isRegular<Account>::value: " << isRegular<Account>::value << std::endl;

    std::cout << std::endl;

}

The output of the program shows it.

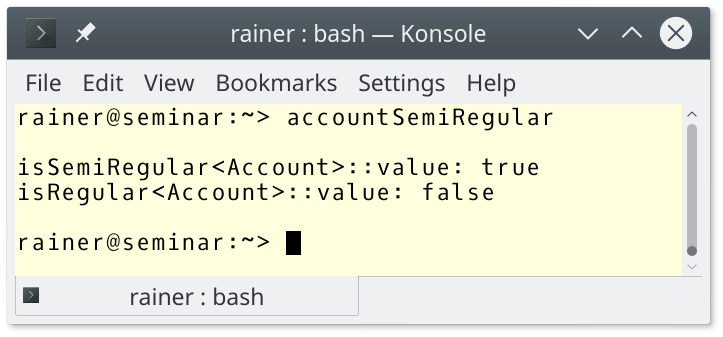
For the details of the program, read my already mentioned post: C++ Core Guidelines: Regular and SemiRegular Types.

By adding the operator == to Account, Account becomes Regular.

// accountRegular.cpp

#include <iostream>

class Account{
public:
    Account() = default;
    Account(double b): balance(b){}
    friend bool operator == (Account const& fir, Account const& sec) {   // (1)
        return fir.getBalance() == sec.getBalance();
    }
    double getBalance() const {
        return balance;
    }
private:
    double balance{0.0};
};

template<typename T>
bool isSmaller(T fir, T sec){
    return fir < sec;
}

int main(){

    std::cout << std::boolalpha << std::endl;
    
    double firDou{};
    double secDou{2014.0};

    std::cout << "isSmaller(firDou, secDou): " << isSmaller(firDou, secDou) << std::endl;

    Account firAcc{};
    Account secAcc{2014.0};

    std::cout << "isSmaller(firAcc, secAcc): " << isSmaller(firAcc, secAcc) << std::endl;
    
    std::cout << std::endl;

}

But Account is still not comparable.

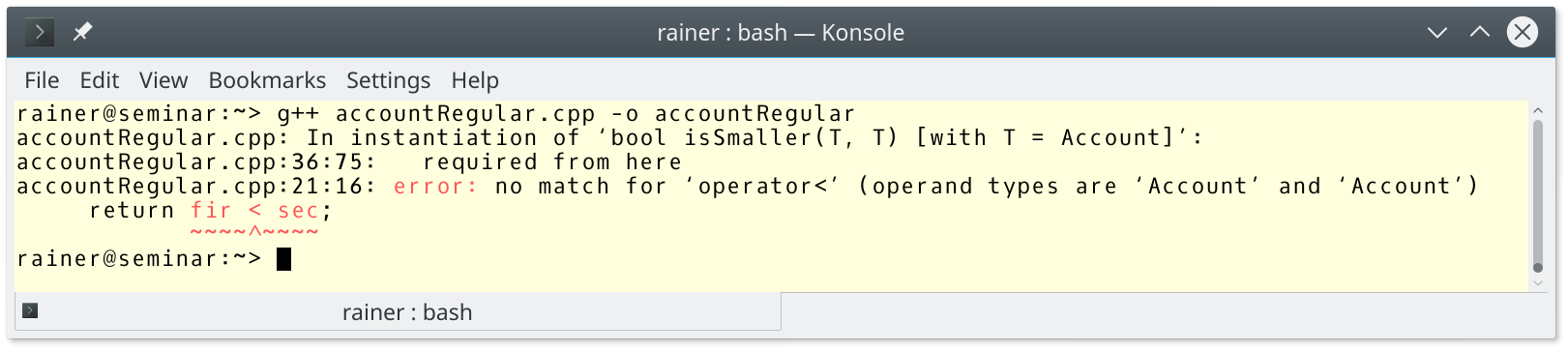
This is the crucial difference between Regular types defined by Alexander Stepanov and the concept of Regular, which we get with C++20. Due to Alexander Stepanov, a Regular type should support a total ordering.

Now, I have come back to my original plan.

Comparing Two Accounts: The Second

The key idea for my variations is that instances of Account should support the generic isSmaller function.

Overloading operator <

Overloading operator < is probably the most obvious way. Even the error message to the program isSmaller.cpp showed it.

// accountIsSmaller1.cpp

#include <iostream>

class Account{
public:
    Account() = default;
    Account(double b): balance(b){}
    friend bool operator == (Account const& fir, Account const& sec) { 
        return fir.getBalance() == sec.getBalance();
    }
    friend bool operator < (Account const& fir, Account const& sec) { 
        return fir.getBalance() < sec.getBalance();
    }
    double getBalance() const {
      return balance;
    }
private:
    double balance{0.0};
};

template<typename T>
bool isSmaller(T fir, T sec){
    return fir < sec;
}

int main(){

    std::cout << std::boolalpha << std::endl;
    
    double firDou{};
    double secDou{2014.0};

    std::cout << "isSmaller(firDou, secDou): " 
              << isSmaller(firDou, secDou) << std::endl;

    Account firAcc{};
    Account secAcc{2014.0};

    std::cout << "isSmaller(firAcc, secAcc): " 
              << isSmaller(firAcc, secAcc) << std::endl;
    
    std::cout << std::endl;

}

The output of this and the next program is the same; therefore, I skip it.

Full Specialisation of isSmaller

If you can not change the definition of Account, you can at least entirely specialize isSmaller for Account.

// accountIsSmaller2.cpp

#include <iostream>

class Account{
public:
    Account() = default;
    Account(double b): balance(b){}
    friend bool operator == (Account const& fir, Account const& sec) { 
        return fir.getBalance() == sec.getBalance();
    }
    double getBalance() const {
      return balance;
    }
private:
    double balance{0.0};
};

template<typename T>
bool isSmaller(T fir, T sec){
    return fir < sec;
}

template<>
bool isSmaller<Account>(Account fir, Account sec){
    return fir.getBalance() < sec.getBalance();
}

int main(){

    std::cout << std::boolalpha << std::endl;
    
    double firDou{};
    double secDou{2014.0};

    std::cout << "isSmaller(firDou, secDou): " 
              << isSmaller(firDou, secDou) << std::endl;

    Account firAcc{};
    Account secAcc{2014.0};

    std::cout << "isSmaller(firAcc, secAcc): " 
              << isSmaller(firAcc, secAcc) << std::endl;
    
    std::cout << std::endl;

}

By the way, a non-generic function bool isSmaller(Account fir, Account sec) would also do the job.

Extend isSmaller with a Binary Predicate

There is another way to extend isSmaller. I spend the generic function an additional type parameter Pred, which should hold the binary predicate. This pattern is often used in the standard template library.

// accountIsSmaller3.cpp

#include <functional>
#include <iostream>
#include <string>

class Account{
public:
    Account() = default;
    Account(double b): balance(b){}
    friend bool operator == (Account const& fir, Account const& sec) { 
        return fir.getBalance() == sec.getBalance();
    }
    double getBalance() const {
      return balance;
    }
private:
    double balance{0.0};
};

template <typename T, typename Pred = std::less<T> >    // (1)
bool isSmaller(T fir, T sec, Pred pred = Pred() ){      // (2)
  return pred(fir, sec);                                // (3)
}

int main(){

    std::cout << std::boolalpha << std::endl;
    
    double firDou{};
    double secDou{2014.0};

    std::cout << "isSmaller(firDou, secDou): " 
              << isSmaller(firDou, secDou) << std::endl;

    Account firAcc{};
    Account secAcc{2014.0};
    
    auto res = isSmaller(firAcc, secAcc,                               // (4)
                         [](const Account& fir, const Account& sec){
                             return fir.getBalance() < sec.getBalance(); 
                         }
    );
    
    std::cout << "isSmaller(firAcc, secAcc): " <<  res << std::endl;
    
    std::cout << std::endl;
    
    std::string firStr = "AAA";
    std::string secStr = "BB";
     
    std::cout << "isSmaller(firStr, secStr): " 
              <<  isSmaller(firStr, secStr) << std::endl;
    
     auto res2 = isSmaller(firStr, secStr,                             // (5)
                           [](const std::string& fir, const std::string& sec){
                               return fir.length() < sec.length(); 
                           }
    );
     
    std::cout << "isSmaller(firStr, secStr): " <<  res2 << std::endl;
    
    std::cout << std::endl;

}

The generic function has std::less<T> as the default ordering (1). The binary predicate Pred is instantiated in line (2) and used in line (3). If you don’t specify the binary predicate, std::less is used. Additionally, you can provide your binary predicates, such as in line (4) or line (5). A lambda function is an ideal fit for this job.

Finally, here is the output of the program:

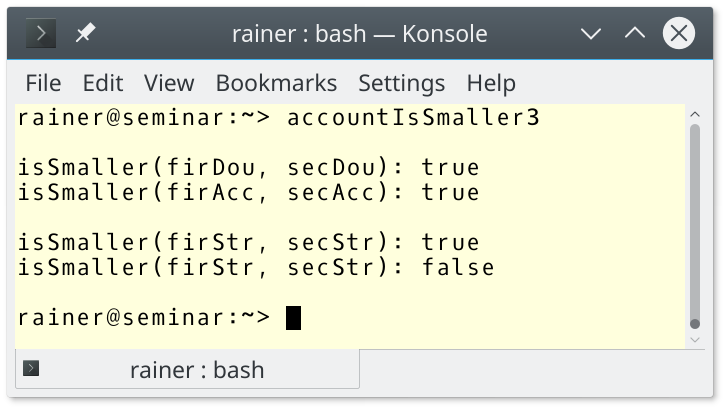
What are the differences between these three techniques?

Comparing two Accounts: The Third

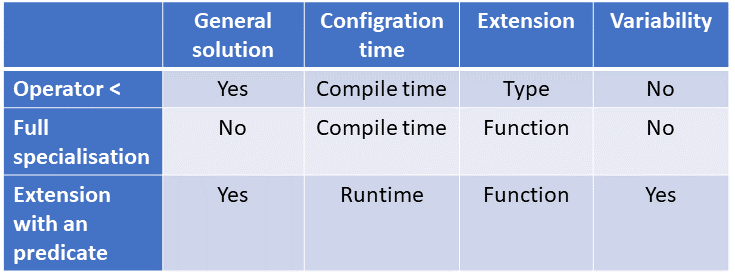
The full specialization is not a general solution because it only works for the function isSmaller. In contrast, the operator < is quite often applicable, and any type can use the predicate. The operator < and the full specialization are static. This means the ordering is defined at compile time and is encoded in the type or the generic function. In contrast, the extension can be invoked with different predicates. This is a runtime decision. The operator < extends the type, the other both variants the function. The extension with a predicate allows it to order your type in various ways. For example, you can compare strings lexicographically or by their length.

Based on this comparison, a good rule of thumb is to implement an operator < for your types and add an extension to your generic functions if necessary. Therefore, your type behaves Regular according to Alexander Stepanov, and supports customized orderings.

What’s next?

The next post is about templates. In particular, it is about template hierarchies.

Post Views: 3,383

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS