Immutable Data
A key to purely functional languages is that their data are immutable. Therefore, assignments such as x= x+1 or ++x are not possible in the purely functional language Haskell. The consequence is that Haskell supports no loops like for, while, or until. They are based on the modification of a loop variable. Haskell does not modify existing data; Haskell creates new data when needed and reuses the old ones.
Immutable data
Immutable data has a lovely property. They are implicitly thread-safe because they miss a necessary condition for a data race. A data race is a state, in which at least two threads access shared data at the same time, and at least one of the threads is a writer.
Quicksort in Haskell
The quicksort algorithm in Haskell shows the immutability of data very nicely.
qsort [] = [] qsort (x:xs) = qsort [y | y <- xs, y < x] ++ [x] ++ qsort [y | y <- xs, y >= x]
The quicksort algorithm qsort consists of two function definitions. The quicksort will be applied to the empty list in the first line. Of course, the result is an empty list. In the second line, there is the general case in which the list consists of at least one element: x: xs. x is the first element in the list, and xs is the reminder by convention.
The quicksort algorithm strategy can be directly applied to Haskell.
- Use the first element of the list x, the so-called pivot element, and make a list with one element out of it: … [x] …
- Add (++) all elements before the list [x] that are smaller than x: qsort [y | y <- xs, y < x]) ++ [x] …
- Add (++) all elements after the list [x] that are equal or bigger than x: …[x] ++ (qsort [y | y <- xs, y >= x])
- The recursion will end if quicksort is applied to the empty list.
Admittedly, the imperative eye is not used to the conciseness of Haskell.
The critical point of the algorithm is that each recursion creates a new list. How does an implementation in C or C++ look like?
Quicksort in C++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
void quickSort(int arr[], int left, int right) { int i = left, j = right; int tmp; int pivot = arr[abs((left + right) / 2)]; while (i <= j) { while (arr[i] < pivot) i++; while (arr[j] > pivot) j--; if (i <= j) { tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; i++; j--; } } if (left < j) quickSort(arr, left, j); if (i < right) quickSort(arr, i, right); } |
No worries. I will not try to explain the algorithm. A simple observation is enough for me. The elements are overwritten in lines 9 – 11. The algorithm works in place and needs, therefore, mutable data. There exists an excellent term in the functional programming for this overwriting: destructive assignment.
That was an implementation of the quicksort algorithm in C. With C++, we can do better if I use the std::partition.
template <class ForwardIt> void quicksort(ForwardIt first, ForwardIt last) { if(first == last) return; auto pivot = *std::next(first, std::distance(first,last)/2); ForwardIt middle1 = std::partition(first, last, [pivot](const auto& em){ return em < pivot; }); ForwardIt middle2 = std::partition(middle1, last, [pivot](const auto& em){ return !(pivot < em); }); quicksort(first, middle1); quicksort(middle2, last); }
But once more. The critical point is that I also use destructive assignment in std::partition. If you look very carefully, the strategy of the C++ version is not so different from that of the Haskell version.
What is the story about immutability in C++?
Immutable data in C++
Using immutable data in C++ is based on the programmer’s discipline. With constant data, template metaprogramming, and constant expressions, you have three ways to express immutability. Options one and two are quite easy to present, but constant expressions deserve more attention.
Constant data
By using the instruction const int value= 1; value becomes immutable data.
 Modernes C++ Mentoring
Modernes C++ Mentoring
Do you want to stay informed: Subscribe.
Template metaprogramming
Template metaprogramming takes place at compile time. At compile time, there is no mutation. Therefore, all values that are calculated at compile time are immutable. Of course, that holds true for the calculation of Factorial::5 at compile time.
template <int N> struct Factorial{ static int const value= N * Factorial<N-1>::value; }; template <> struct Factorial<1>{ static int const value = 1; }; std::cout << Factorial<5>::value << std::endl; std::cout << 120 << std::endl;
If the short notice to template programming was too short, please read the post Functional in C++98.
But now, back into the future of C++: constant expressions.
Constant expressions
C++11 supports constant expressions. With C++14, you can declare functions as constant expressions that behave almost as usual functions.
C++ supports constant expressions in three variations: variables, user-defined types, and functions. The special feature of constant expressions is that they can be evaluated at compile time.
- By using constexpr double pi= 3.14 pi becomes a constant expression. pi is, therefore, implicit const and has to be initialized by a constant expression: 3.14.
- There are a few restrictions for a user-defined type so that the instances of the user-defined type become constant expressions. For example, the constructor has to be empty and have a constant expression. The instance can only use methods that are constant expressions. Of course, you can not invoke a virtual method at compile time. If a user-defined type fulfills all requirements, you can instantiate and use its objects simultaneously.
- To execute functions in C++14 at compile time, they must follow a few rules. First, their arguments must be constant expressions. Second, they can not use static or thread-local data.
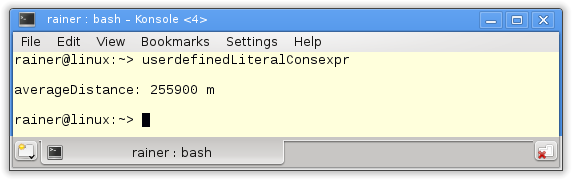
The following example shows the power of constant expressions. I use user-defined literals to calculate all distances at compile time.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
// userdefinedLiteralsConstexpr.cpp #include <iostream> namespace Distance{ class MyDistance{ public: constexpr MyDistance(double i):m(i){} friend constexpr MyDistance operator+(const MyDistance& a, const MyDistance& b){ return MyDistance(a.m + b.m); } friend constexpr MyDistance operator-(const MyDistance& a,const MyDistance& b){ return MyDistance(a.m - b.m); } friend constexpr MyDistance operator*(double m, const MyDistance& a){ return MyDistance(m*a.m); } friend constexpr MyDistance operator/(const MyDistance& a, int n){ return MyDistance(a.m/n); } friend std::ostream& operator<< (std::ostream &out, const MyDistance& myDist){ out << myDist.m << " m"; return out; } private: double m; }; namespace Unit{ constexpr MyDistance operator "" _km(long double d){ return MyDistance(1000*d); } constexpr MyDistance operator "" _m(long double m){ return MyDistance(m); } constexpr MyDistance operator "" _dm(long double d){ return MyDistance(d/10); } constexpr MyDistance operator "" _cm(long double c){ return MyDistance(c/100); } } } constexpr Distance::MyDistance getAverageDistance(std::initializer_list<Distance::MyDistance> inList){ auto sum= Distance::MyDistance{0.0}; for (auto i: inList) sum = sum + i ; return sum/inList.size(); } using namespace Distance::Unit; int main(){ std:: cout << std::endl; constexpr auto work= 63.0_km; constexpr auto workPerDay= 2 * work; constexpr auto abbrevationToWork= 5400.0_m; constexpr auto workout= 2 * 1600.0_m; constexpr auto shopping= 2 * 1200.0_m; constexpr auto distPerWeek1= 4*workPerDay-3*abbrevationToWork+ workout+ shopping; constexpr auto distPerWeek2= 4*workPerDay-3*abbrevationToWork+ 2*workout; constexpr auto distPerWeek3= 4*workout + 2*shopping; constexpr auto distPerWeek4= 5*workout + shopping; constexpr auto averageDistance= getAverageDistance({distPerWeek1,distPerWeek2,distPerWeek3,distPerWeek4}); std::cout << "averageDistance: " << averageDistance << std::endl; // 255900 m std::cout << std::endl; } |
I will not repeat myself by explaining constant expressions and user-defined literals in detail. I have already done it in the posts to constexpr and user-defined literals. I want to make only two observations:
- By declaring constexpr, all variables, class MyDistance instances, and functions become constant expressions. The compiler performs, therefore, the necessary operations at compile time.
- All variables, instances, and functions – excluding std::cout – are constant expressions. That means the entire program will be executed at compile time. Therefore, all used variables and instances are immutable. Only the output of the program 255900 m in line 77 is performed at run time.
What’s next?
Pure functions are pretty similar to mathematical functions. They are why Haskell and template metaprogramming is called pure functional languages. But what restrictions do a purely functional language have to fight with? These will be my topic for the next post.
Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, Honey Sukesan, bruce_lee_wayne, Silviu Ardelean, schnapper79, Seeker, and Sundareswaran Senthilvel.
Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.
| My special thanks to Embarcadero |  |
| My special thanks to PVS-Studio |  |
| My special thanks to Tipi.build |  |
| My special thanks to Take Up Code |  |
| My special thanks to SHAVEDYAKS |  |
Modernes C++ GmbH
Modernes C++ Mentoring (English)
Rainer Grimm
Yalovastraße 20
72108 Rottenburg
Mail: schulung@ModernesCpp.de
Mentoring: www.ModernesCpp.org





Leave a Reply
Want to join the discussion?Feel free to contribute!