Function Templates

A function template is a family of functions. In this post, I want to dive deeper into function templates.

Here is a short reminder to get you on the same page.

When you instantiate a function template such as max for int and double

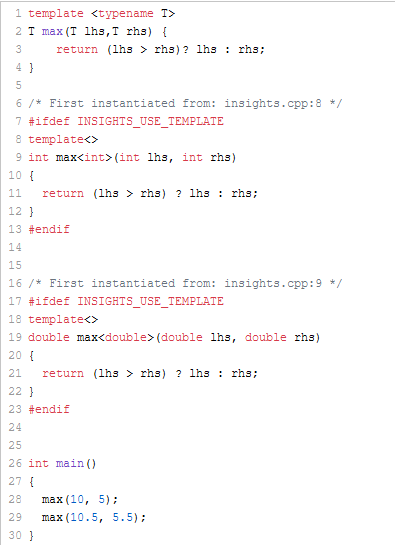
template <typename T>
T max(T lhs,T rhs) {
    return (lhs > rhs)? lhs : rhs;
}

int main() {
  
    max(10, 5);
    max(10.5, 5.5);
  
}

the compiler generates a fully specialized function template for int and double: max<int> and max<double>. The generic part is, in both cases, empty: template<> Thanks to C++ Insights, here are the insights.

Okay, now I can dive into the details. What happens when function templates and non-template functions (in short functions) overload?

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

Overloading of Function Templates and Functions

Let me use the function max once more. This time I instantiate it for float and double, and I provide a function max also taking doubles.

Here is my following example:

template <typename T>
T max(T lhs,T rhs) {
    return (lhs > rhs)? lhs : rhs;
}

double max(double lhs, double rhs) {
    return (lhs > rhs)? lhs : rhs;
}

int main() {
  
    max(10.5f, 5.5f); // (1)
    max(10.5, 5.5);   // (2)
  
}

You may guess my question. What happens in lines (1) and (2)? Here are a few questions?

Line (1): Does the compiler choose the function template or the function and promote the float to double.
Line (2): Either the function and the function templates are ideal fits. This seems to be ambiguous and may cause a compiler error.

The answer to questions is pretty intuitive and follows the general rule in C++. The compiler chooses the best-fitting function.

Line (1): The function template is the better fit because the function would require a promotion from float to double.
Line (2): The function template and the function are ideal fits. In this case, an additional rule kicks in. When both are equally good fits, the compiler prefers the function.

As before, C++ Insights helps to visualize this process.

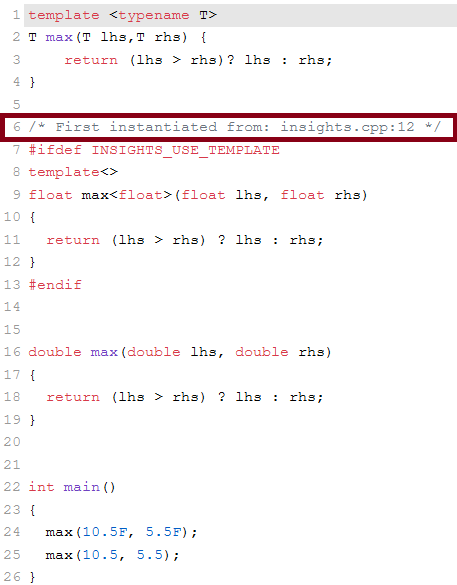
The screenshot shows it explicitly. Only the use of the function template max with float (line 2) triggers the instantiations of the function template.

Let’s go further in our journey through the basics of function templates.

First disclaimer: I ignore concepts in this post.

Different Template Arguments

Let me use my function template max with two values having different types.

template <typename T>
T max(T lhs,T rhs) {
    return (lhs > rhs)? lhs : rhs;
}

int main() {
  
    max(10.5f, 5.5);
  
}

Let’s try it out on C++ Insights:

Wow! What is happening here? Why is the float not promoted to a double? Honestly, the compiler thinks differently, and let me explain how.

The compiler deduces the template argument from the function argument if possible. In this case, it’s possible.
The compiler does this process of template argument deduction for each function argument.
For 10.5f the compiler deduces float for T, for 5.5 the compiler deduces double for T.
Of course, T cannot be float and double at the same time. Because of this ambiguity, the compilation failed.

Second disclaimer: I simplified the process of template argument deduction. I will write an additional post about template argument deduction for function templates and class templates in a future post.

Of course, we want to compare values of different types.

Two Type Parameters

The solution seems to be straightforward. I introduce a second type parameter.

template <typename T, typename T2>
??? max(T lhs,T2 rhs) {
    return (lhs > rhs)? lhs : rhs;
}

int main() {
  
    max(10.5f, 5.5);
  
}

This is easy! Right? But there is a severe problem. Do you see the three question marks as return type? This problem typically occurs when your function template has more than one type parameter. What should be the return type?

In this concrete case, should the return type be T, T2, or a Type R derived from T and T2? This task was challenging before C++11, but it is pretty easy with C++11.

Here are a few solutions I have in mind:

// automaticReturnTypeDeduction.cpp

#include <type_traits>

template <typename T1, typename T2>      // (1)
typename std::conditional<(sizeof(T1) > sizeof(T2)), T1, T2>::type max1(T1 lhs,T2 rhs) {
    return (lhs > rhs)? lhs : rhs;
}

template <typename T1, typename T2>      // (2)
typename std::common_type<T1, T2>::type max2(T1 lhs,T2 rhs) {
    return (lhs > rhs)? lhs : rhs;
}

template <typename T1, typename T2>     // (3)
auto max3(T1 lhs,T2 rhs) {
    return (lhs > rhs)? lhs : rhs;
}

int main() {
  
    max1(10.5f, 5.5);                  
    max2(10.5f, 5.5);                  
    max3(10.5f, 5.5);                  
  
}

The first two versions max1 (line 1) and max2 (line 2) are based on the type-traits library. The third version max3 (line 3) uses the automatic type deduction of auto.

max1 (line 1): typename std::conditional<(sizeof(T1) > sizeof(T2)), T1, T2>::type returns the type T1, or T2 that is bigger. std::conditional is a kind of compile-time ternary operator.
max2 (line2): typename td::common_type<T1, T2>::type returns the common type of the types T1 and T2. std::common_type can accept an arbitrary number of arguments.
max3 (line3): auto should be self-explanatory.

Maybe you are irritated by the typename in-front of the return type of the function template max1 and max2. T1 and T2 are dependent names. What is a dependent name? A dependent name is essentially a name that depends on a template parameter. In this case, we have to give the compiler a hint that T1 and T2 are types. Essentially, they can also be non-types or templates.

Third disclaimer: I write in an additional post about dependent types.

Let’s see what C++ Insights provides. I only show the template instantiations. If you want to analyze the entire program, follow this link: C++ Insights.

max1(line 1): You can only guess the return type. In the return statement, the smaller type (float) is converted to double.
max2(line 2): As for max1, the return statement gives an idea about the return type: the float value is converted to double.

max3 (line 3): Now, we can see the return type explicitly. It is a double.

What’s next?

In this installment, I solved the challenge of different types of function arguments by using more than one type parameter. Next time, I will take a different approach and explicitly specify the template arguments.

Post Views: 6,859

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS