C++20: Define Concepts

With this post, I start my last fascinating topic to concepts: define your concepts. Consequentially, I answer the questions I opened in previous posts.

First and foremost, most of the concepts I define are already available in the C++ 20 draft. Therefore, there is no need to define them. To distinguish my concepts from the predefined concepts, I capitalize them. My previous post gave an overview of the predefined concepts: C++20: Concepts – Predefined Concepts.

Defining concepts

There are two typical ways to define concepts: direct definition or requires-expressions.

Direct definition

The syntactic form changed a little bit from the syntax based on the concepts TS (Technical Specification) to the proposed syntax for the C++20 standard.

Concepts TS

template<typename T>
concept bool Integral(){
    return std::is_integral<T>::value;
}

C++20 standard

template<typename T>
concept Integral = std::is_integral<T>::value;

The C++20 standard syntax is less verbose. Both used under the hood the function std::is_integral<T>::value from the C++11 type-traits library. T fulfills the concept if the compile-time predicate std::integral<T>::value evaluates to true. Compile-time predicate means that the function runs at compile-time and returns a boolean. Since C++17, you can write std::integral<T>::value less verbose: std::integral_v<T>.

I’m unsure if the two terms variable concept for direct definition and function concept for requires-expressions are still used. Still, they help to keep the difference between the direct definition and the requires-expressions in mind.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

I skip the example to the usage of the concept Integral. If you are curious, read my previous post: C++ 20: Concepts, the Placeholder Syntax.

Requires-expressions

Analogous to the direct definition, the syntax of requires-expressions also changed from the concepts TS to the proposed draft C++20 standard.

Concepts TS

template<typename T>
concept bool Equal(){
    return requires(T a, T b) {
        { a == b } -> bool;
        { a != b } -> bool;
   };
}

C++20 standard

template<typename T>
concept Equal =
    requires(T a, T b) {
        { a == b } -> bool;
        { a != b } -> bool;
    };

As before, the C++20 syntax is more concise. T fulfills the concept if the operator == and != are overloaded and return a boolean. Additionally, the types of a and b have to be the same.

The concept Equal

Now, it’s time to use the concept Equal:

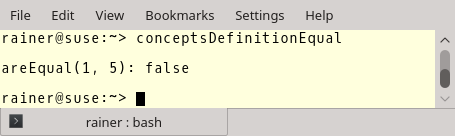
// conceptsDefintionEqual.cpp

#include <iostream>

template<typename T>
concept Equal =
    requires(T a, T b) {
        { a == b } -> bool;
        { a != b } -> bool;
};


bool areEqual(Equal auto a, Equal auto b) {                     // (1)            
  return a == b;
}

/*

struct WithoutEqual{
  bool operator==(const WithoutEqual& other) = delete;
};

struct WithoutUnequal{
  bool operator!=(const WithoutUnequal& other) = delete;
};

*/

int main() {
  
  std::cout << std::boolalpha << std::endl;
  
  std::cout << "areEqual(1, 5): " << areEqual(1, 5) << std::endl;
  
  /*
  
  bool res = areEqual(WithoutEqual(),  WithoutEqual());
  
  bool res2 = areEqual(WithoutUnequal(),  WithoutUnequal());
  
  */
  
  std::cout << std::endl;
  
}

I used the concept of Equal in the function areEqual (line 1). To remind you. Using a concept as a function parameter, the compiler creates a function template under the hood, with the concept specified constraints on the parameters. To get more information on this concise syntax, read my post: C++ 20: Concepts, the Placeholder Syntax.

The output is not so exciting:

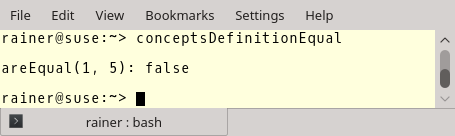
Now, it has become exciting. What happens if I use the types WithoutEqual and WithoutUnequal. I intentionally set the == operator and the != operator to delete. The compiler complains immediately that both types do not fulfill the concept of Equal.

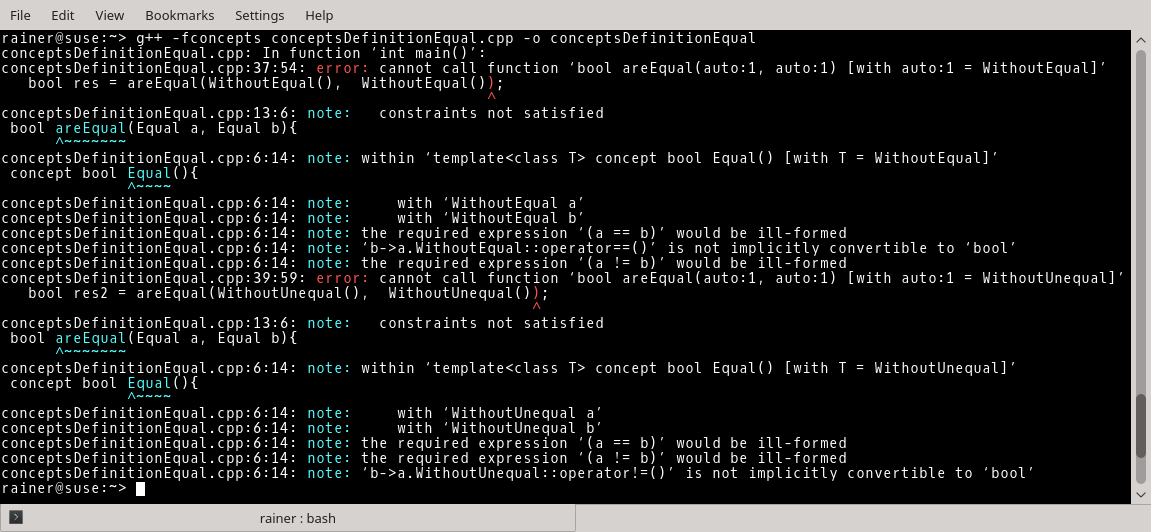
When you look carefully at the error message, you see the reason: (a == b) would be ill-formed, and (a != b) would be ill-formed.

Before I continue, I have to make a short detour. You can skip the detour if you don’t want to compile the program.

The Implementation status of concepts

I faked the output of the program conceptsDefinitonEqual.cpp. The output is from the Concepts TS implementation of GCC. Currently, no C++20 standard-conforming implementation of the concepts syntax is available.

The latest Microsoft compiler supports the C++20 syntax for defining concepts but not the placeholder syntax I used for the function areEqual.
The GCC compiler supports the placeholder syntax I used but not the C++20 draft syntax for defining concepts.

From Equal to Ord

In the previous post, C++20: Two Extremes and the Rescue with Concepts, I mentioned that concepts at first reminded me of Haskell’s type classes. Type classes in Haskell are interfaces for similar types. The main difference to concepts is, that a type such as Int in Haskell has to be an instance of a type class and, therefore, to implement the type class. On the contrary, the compiler checks with concepts if a type fulfills a concept.

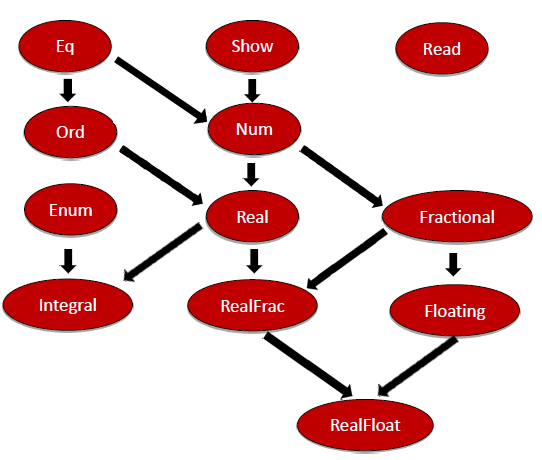
Here is a part of the Haskell type class hierarchy.

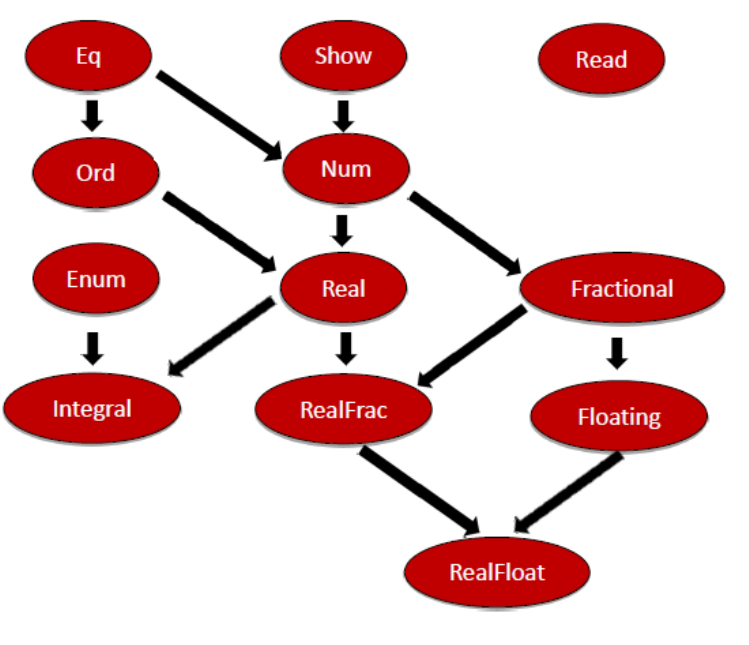
This is my crucial observation. Haskell supports the type class Eq. When you compare the definition of the type class Eq and the concept Equal, they look quite similar.

The type class Eq

class Eq a where
    (==) :: a -> a -> Bool
    (/=) :: a -> a -> Bool

The concept Equal

template<typename T>
concept Equal =
    requires(T a, T b) {
        { a == b } -> bool;
        { a != b } -> bool;
    };

Haskell’s type class requires from its instances, such as Int,

that they have the equal == and inequal /= operation that returns a Bool.
that both operations take two arguments (a -> a) of the same type.

Let’s look once more at the type class hierarchy of Haskell. The type class Ord is a refinement of the type class Eq. The definition of Ord makes this clear.

class Eq a => Ord a where
    compare :: a -> a -> Ordering
    (<) :: a -> a -> Bool
    (<=) :: a -> a -> Bool
    (>) :: a -> a -> Bool
    (>=) :: a -> a -> Bool
    max :: a -> a -> a

The most exciting point about the definition of the type class Ord is their first line. An instance of the type class Ord has to be already an instance of the type class Eq. Ordering is an enumeration having the values EQ, LT, and GT. This refinement of type classes is exquisite.

Here is the challenge for the next post. Can concepts be refined in a similarly elegant way?

What’s next?

In my next post, I accept the challenge to refine the concept of Equal. Additionally, I write about the essential concepts Regular and Semiregular, and I define them.

Post Views: 6,822

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS