constexpr Functions

constexpr functions are functions that can be executed at compile time. Sounds not so thrilling. But it is. Trust me. You can perform with constexpr functions a lot of calculations at compile time. Therefore, the calculation result is at runtime as a constant in ROM available. In addition, constexpr functions are implicitly inline.

The syntax of constexpr functions was significantly improved with the change from C++11 to C++14. The positive list from C++11 is with C++14 negative. In C++11, you had to remember which feature you can use in a constexpr functions. With C++14, you only have to remember which feature you can’t use in a constexpr function.

C++11

For constexpr functions, there are a few restrictions:

The function

has to be non-virtual.
has to have arguments and a return value of a literal type. Literal types are the types of constexpr variables.

The restriction goes on with the function body. The key points are that

it has to be defined with the keyword default or delete or
can only have one return statement.

Is it possible to define a meaningful function with such restrictions? Because constexpr functions can not have a conditional like if or a loop. Yes. Look at the constexpr functions in the post Constant expressions with constexpr. Only the function getAverageDistance requires the C++14 standard.

Fortunately, we have the ternary operator and recursion in C++. Therefore, I can implement the gcd algorithm as a constexpr function.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

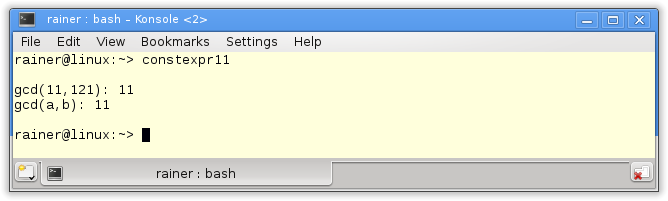
// constexpr11.cpp

#include <iostream>

constexpr int gcd(int a, int b){
  return (b== 0) ? a : gcd(b, a % b);
}

int main(){
  
  std::cout << std::endl;
  
  constexpr int i= gcd(11, 121);
  
  int a= 11;
  int b= 121;
  int j= gcd(a,b);

  std::cout << "gcd(11,121): " << i << std::endl;
  std::cout << "gcd(a,b): " << j << std::endl;
  
  std::cout << std::endl;
 
}

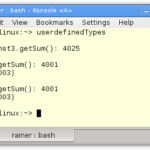
I implemented in line 6 the Euclidean algorithm with the help of the ternary operator and recursion. Comprehensible code looks different. Of course, I can invoke the gcd function with arguments that are non-constant expressions (lines 15 and 16). Therefore, the result will be calculated at runtime and can only be taken by a non-constant expression (line 17).

The result is a little bit boring. But wait for a second.

A glimpse of the assembler’s instructions is quite enlightening.

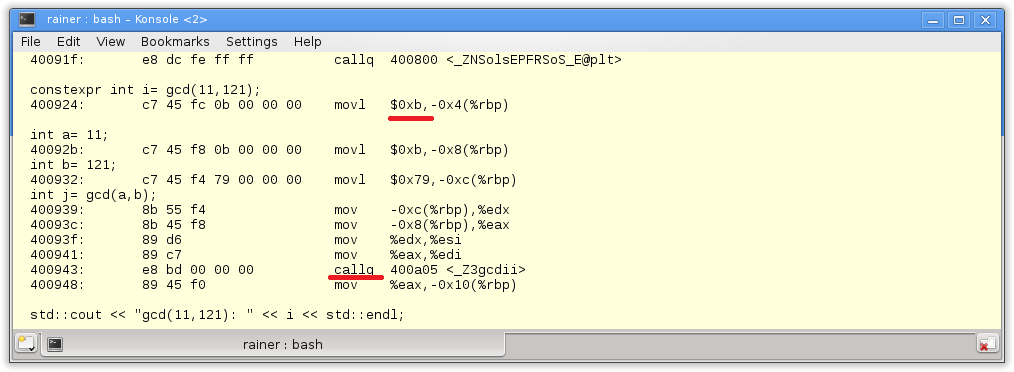
The call of the constexpr function in line 13 causes the result of gcd(11, 121) to be available in the object file. This is opposite to the function call in line 17. At first, the processor has to push the variables on the stack (Instructions 400939 – 400941 in the object dump). Second, the processor has to invoke (callq) the function and store the result in the variable j (400948). What a difference!

Of course, you can define more powerful constexpr functions by calling ternary operators from ternary operators. This technique is Turing complete. So you can compute all that is computable. Fortunately, you don’t have to do that. You can use the C++14 constexpr functions, which behave almost like ordinary functions.

C++14

constexpr can have

conditional jump instructions or loop instructions.
more than one instruction.
constexpr functions.
fundamental data types that have to be initialized with a constant expression.

The difference between ordinary functions to constexpr functions in C++14 is minimal. constexpr functions can not have static or thread_local data. Either can they have a try block or a goto instruction? Therefore, it’s quite easy to implement the gcd algorithm in C++14 as a constexpr function.

// constexpr14.cpp

#include <iostream>

constexpr auto gcd(int a, int b){
  while (b != 0){
    auto t= b;
    b= a % b;
    a= t;
  }
  return a;
}

int main(){
  
 std::cout << std::endl;
  
  constexpr int i= gcd(11,121);
  
  int a= 11;
  int b= 121;
  int j= gcd(a,b);

  std::cout << "gcd(11,121): " << i << std::endl;
  std::cout << "gcd(a,b): " << j << std::endl;
  
  std::cout << std::endl;
 
}

I skip the output of the program because it’s identical to the output of the C++11 variant.

Thanks to a discussion with Odin Holmes in the Facebook group of this blog Modernes C++ I want to present a very interesting use case for constexpr functions.

Pure functions

You can execute constexpr functions at runtime. If you take the return value of a constexpr function by a constant expression, the compiler will perform the function at compile time. The question is: Is there a reason to perform a constexpr function at runtime? Of course, you have the constexpr function, so you can use it at runtime. But there is a much more convincing reason.

A constexpr function can be potentially performed at compile time. There is no state at compile time. At compile time, we are in a pure functional sublanguage of the imperative programming language C++. In particular, that means that at compile time, executed functions have to be pure functions. When you use this constexpr function at runtime, the function keeps pure. Pure functions always return the same result when given the same arguments. Pure functions are like infinitely large tables from which you get your value. Referential transparency is the guarantee that an expression always returns the same result when given the same arguments.

Pure functions have a lot of advantages:

The result can replace the function call.
The execution of pure functions can automatically be distributed to other threads.
The function call can be reordered.
They can easily be refactored.

The last three points hold because pure functions have no state and have, therefore, no dependency on the environment. Pure functions are often called mathematical functions.

There are a lot of good reasons to use constexpr functions. The table shows the critical points of pure and impure functions.

I will write in a few weeks about functional programming in C++. Then I will explain the details of pure functions and pure functional programming.

Pure and purer

I want to stress one point. constexpr functions are not per se pure. Thanks to Marcel Wid, who made me aware of this. constexpr functions are a lot purer than ordinary functions. E.g., you can only invoke a constexpr function in a constexpr function. Those who want only to use pure functions should study Haskell. The exceptionally well-written introduction to Haskell Learn You a Haskell For Great Good from Miran Lipovaca is available online.

What’s next?

In the post More and more save, I successively optimized the gcd algorithm. Thanks to the type-traits library and static_assert, this was quite impressive. But that was not the whole story about the type traits. By analyzing the type system of your code, you can write self-optimizing programs. How? Read the next post.

{tooltip} {end-texte} Go to Leanpub/cpplibrary “What every professional C++ programmer should know about the C++ standard library”. {end-tooltip} Get your e-book. Support my blog.

Post Views: 9,075

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery,and Matt Godbolt.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS