Automatic Return Type (C++98)
Depending on the used C++ standard, there are different ways to return the correct return type of a function template. In this post, I start with traits (C++98), continue in my next post with C++11/14, and end with concepts (C++20).
Here is the challenge for today’s post.
template <typename T, typename T2> ??? sum(T t, T2 t2) { return t + t2; }
When you have a function template, such as sum with at least two type parameters, you can not decide, in general, the return type of the function. Of course, sum should return the type that the arithmetic operation t + t2 provides. Here are a few examples using run-time type information (RTTI) with std::type_info.
// typeinfo.cpp #include <iostream> #include <typeinfo> int main() { std::cout << '\n'; std::cout << "typeid(5.5 + 5.5).name(): " << typeid(5.5 + 5.5).name() << '\n'; std::cout << "typeid(5.5 + true).name(): " << typeid(5.5 + true).name() << '\n'; std::cout << "typeid(true + 5.5).name(): " << typeid(true + 5.5).name() << '\n'; std::cout << "typeid(true + false).name(): " << typeid(true + false).name() << '\n'; std::cout << '\n'; }
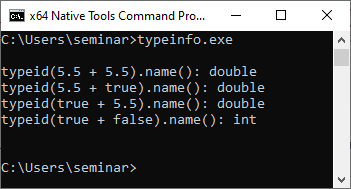
I executed the program on Windows using MSVC because MSVC produces in contrast to GCC or Clang human-readable names.
 Modernes C++ Mentoring
Modernes C++ Mentoring
Do you want to stay informed: Subscribe.
Adding two doubles returns a double, adding a double and a bool returns a bool, and adding two bools returns an int.
I use in my examples only arithmetic types. You must extend my solutions if you want to apply my examples to user-defined that support arithmetic operations.
Now, my journey starts with C++98.
C++98
Honestly, C++98 provides no general solution for returning the correct type. Essentially, you must implement the type-deduction rules using a technique called traits, also known as template traits. A traits class provides valuable information about template parameters and can be used instead of the template parameters.
The following class ResultType provides a type-to-type mapping using full template specialization.
// traits.cpp #include <iostream> #include <typeinfo> template <typename T, typename T2> // primary template (1) struct ReturnType; template <> // full specialization for double, double struct ReturnType <double, double> { typedef double Type; }; template <> // full specialization for double, bool struct ReturnType <double, bool> { typedef double Type; // (2) }; template <> // full specialization for bool, double struct ReturnType <bool, double> { typedef double Type; }; template <> // full specialization for bool, bool struct ReturnType <bool, bool> { typedef int Type; }; template <typename T, typename T2> typename ReturnType<T, T2>::Type sum(T t, T2 t2) { // (3) return t + t2; } int main() { std::cout << '\n'; std::cout << "typeid(sum(5.5, 5.5)).name(): " << typeid(sum(5.5, 5.5)).name() << '\n'; std::cout << "typeid(sum(5.5, true)).name(): " << typeid(sum(5.5, true)).name() << '\n'; std::cout << "typeid(sum(true, 5.5)).name(): " << typeid(sum(true, 5.5)).name() << '\n'; std::cout << "typeid(sum(true, false)).name(): " << typeid(sum(true, false)).name() << '\n'; std::cout << '\n'; }
Line (1) is the primary template or general template. The primary template has to be declared before the following full specializations. A declaration such as in line 1 is acceptable if the primary template is unnecessary. The following lines provide the full specializations for <double, double> , for <double, bool>, for <bool, double>, and for <bool, bool>. You can read more details about template specialization in my previous posts:
- Template Specialization
- Template Specialization – More Details about Class Templates
- Full Specialization of Function Templates
The critical observation in the various full specializations of ReturnType is that they all have an alias Type such as typedef double Type (line 2). This alias is the return type of the function template sum (line 3): typename ReturnType<T, T2>::type.
The traits work as expected.
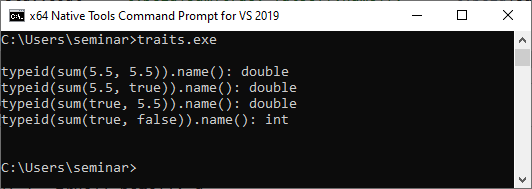
You may be wondering why I used typename in the return type expression of the function template sum. At least one reader of my previous post about Dependent Names asked me when to apply typename or .template to templates. The short answer is that the compiler can not decide if the expression ReturnType<T, T2>::Type is a type (such as in this case), a non-type, or a template. Using typename before ReturnType<T, T2>::Type gives the compiler the crucial hint. You can read the long answer in my previous post Dependent Names.
Missing Overload
Initially, I wanted to continue my post and write about C++11. Still, I assume you have another question: What happens when I invoke the function template sum with arguments for which not partial template specialization is defined? Let me try it out with sum(5.5f, 5).
// traitsError.cpp #include <iostream> #include <typeinfo> template <typename T, typename T2> // primary template struct ReturnType; template <> // full specialization for double, double struct ReturnType <double, double> { typedef double Type; }; template <> // full specialization for double, bool struct ReturnType <double, bool> { typedef double Type; }; template <> // full specialization for bool, double struct ReturnType <bool, double> { typedef double Type; }; template <> // full specialization for bool, bool struct ReturnType <bool, bool> { typedef int Type; }; template <typename T, typename T2> typename ReturnType<T, T2>::Type sum(T t, T2 t2) { return t + t2; } int main() { std::cout << '\n'; std::cout << "typeid(sum(5.5f, 5.5)).name(): " << typeid(sum(5.5f, 5.5)).name() << '\n'; std::cout << '\n'; }
Many C++ programmers expect that the float value 5.5f is converted to an double and the full specialization for <double, double> is used.
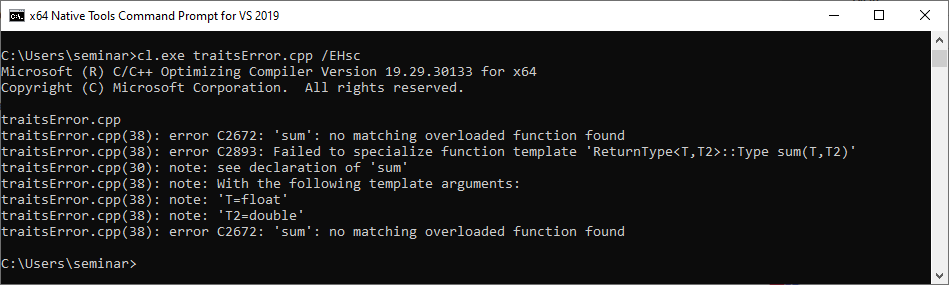
NO! The types must match exactly. The MSVC compiler gives an exact error message. There is no overload sum for T = float and T2 = double available. The primary template is not defined and can not be instantiated.
Types do not convert; only expressions such as values can be converted: double res = 5.5f + 5.5;
Default Return Type
When you make out of the declaration of the primary template a definition, the primary template becomes the default case. Consequently, the following implementation of ReturnType uses long double as the default return type.
// traitsDefault.cpp #include <iostream> #include <typeinfo> template <typename T, typename T2> // primary template struct ReturnType { typedef long double Type; }; template <> // full specialization for double, double struct ReturnType <double, double> { typedef double Type; }; template <> // full specialization for double, bool struct ReturnType <double, bool> { typedef double Type; }; template <> // full specialization for bool, double struct ReturnType <bool, double> { typedef double Type; }; template <> // full specialization for bool, bool struct ReturnType <bool, bool> { typedef int Type; }; template <typename T, typename T2> typename ReturnType<T, T2>::Type sum(T t, T2 t2) { return t + t2; } int main() { std::cout << '\n'; std::cout << "typeid(sum(5.5, 5.5)).name(): " << typeid(sum(5.5, 5.5)).name() << '\n'; std::cout << "typeid(sum(5.5, true)).name(): " << typeid(sum(5.5, true)).name() << '\n'; std::cout << "typeid(sum(true, 5.5)).name(): " << typeid(sum(true, 5.5)).name() << '\n'; std::cout << "typeid(sum(true, false)).name(): " << typeid(sum(true, false)).name() << '\n'; std::cout << "typeid(sum(5.5f, 5.5)).name(): " << typeid(sum(5.5f, 5.5)).name() << '\n'; std::cout << '\n'; }
The invocation of sum(5.5f, 5.f) causes the instantiation of the primary template.

What’s next?
In C++11, there are various ways to deduce the return type automatically. C++14 adds syntactic sugar to these techniques, and C++20 enables it to write it very explicitly. Read more about the improvements in my next post.
Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, Honey Sukesan, bruce_lee_wayne, Silviu Ardelean, schnapper79, Seeker, and Sundareswaran Senthilvel.
Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.
| My special thanks to Embarcadero |  |
| My special thanks to PVS-Studio |  |
| My special thanks to Tipi.build |  |
| My special thanks to Take Up Code |  |
| My special thanks to SHAVEDYAKS |  |
Modernes C++ GmbH
Modernes C++ Mentoring (English)
Rainer Grimm
Yalovastraße 20
72108 Rottenburg
Mail: schulung@ModernesCpp.de
Mentoring: www.ModernesCpp.org





Leave a Reply
Want to join the discussion?Feel free to contribute!