Template Metaprogramming – How it All Started

Metaprogramming is programming on programs. C++ applies metaprogramming at compile time. It started in C++98 with template metaprogramming, was formalized in C++11 with the type-traits library, and since C++11 has steadily improved. The main driving force is constant expressions. In this post, I want to write about its roots.

In writing about template metaprogramming, I want to demystify its techniques. This demystification helps you to understand better the functions of the type-traits library and, in particular, appreciate constexpr. Most of the bad reputation of template metaprogramming is that you may get error messages of epic length. Template metaprogramming was not designed; it started with an accident.

The Accident

In 1994, Erwin Unruh from Siemens presented at a C++ committee meeting a program that didn’t compile. Here is probably the most famous program that never compiled successfully.

// Prime number computation by Erwin Unruh
template <int i> struct D { D(void*); operator int(); };

template <int p, int i> struct is_prime {
    enum { prim = (p%i) && is_prime<(i > 2 ? p : 0), i -1> :: prim };
    };

template < int i > struct Prime_print {
    Prime_print<i-1> a;
    enum { prim = is_prime<i, i-1>::prim };
    void f() { D<i> d = prim; }
    };

struct is_prime<0,0> { enum {prim=1}; };
struct is_prime<0,1> { enum {prim=1}; };
struct Prime_print<2> { enum {prim = 1}; void f() { D<2> d = prim; } };
#ifndef LAST
#define LAST 10
#endif
main () {
    Prime_print<LAST> a;
    }

Erwin Unruh used the Metaware Compilers, but the program is not valid for C++ anymore. A newer variant from the author is here. Okay, why is this program so famous? Let’s look at the original error messages that wrote type as txpe.

I highlighted the important parts in red. I think you see the pattern. The program calculates at compile time the first prime numbers until 30. This means template instantiation can be used to do math at compile time. It is even better. Template metaprogramming is Turing-complete, and can, therefore, be used to solve any computational problem. (Of course, Turing completeness holds only in theory for template metaprogramming because the recursion instantiation depth (at least 1024 with C++11) and the length of the names generated during template instantiation provide some limitations.)

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

How does the magic work?

Let me decompose what is going on step by step.

Calculating at Compile Time

Calculating the factorial of a number is the “Hello World” of template metaprogramming.

// factorial.cpp

#include <iostream>

template <int N>                                                                 // (2)
struct Factorial{
    static int const value = N * Factorial<N-1>::value;
};

template <>                                                                      // (3)
struct Factorial<1>{
    static int const value = 1;
};

int main(){
    
    std::cout << '\n';
    
    std::cout << "Factorial<5>::value: " << Factorial<5>::value << '\n';    // (1)
    std::cout << "Factorial<10>::value: " << Factorial<10>::value << '\n';  // (4)
    
    std::cout << '\n';

}

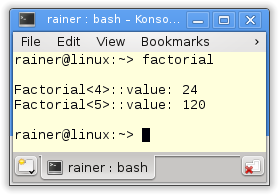
The call factorial<5>::value in line (1) causes the instantiation of the primary or general template in line (2). During this instantiation, Factorial<4>::value will be instantiated. This recursion will end if the fully specialized class template Factorial<1> kicks in in line (3). Maybe, you like it more pictorial.

Here is the output of the program:

Thanks to C++ Insights and Compiler Explorer, you can and should analyze the program further. This should help to build your intuition about template instantiation and template metaprogramming.

Let me start with C++ Insights:

C++ Insights

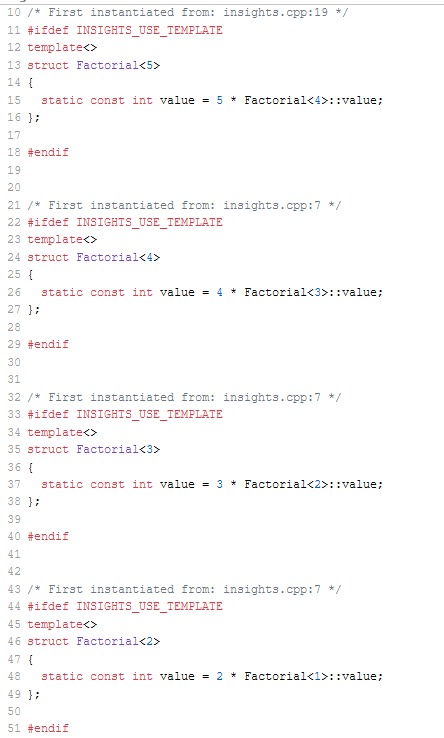
The call Factorial<5>::value (line 1) causes the instantiation of the class template for the numbers 5 to 2. The full specialization for 1 is already available. The call Factorial<10>::value (line 2) causes the instantiation of the function template for the numbers 10 – 6 because all other fully specialized function templates are already available. The following output shows the instantiation for the numbers 5 to 2.

Now, my analysis continues with the Compiler Explorer.

Compiler Explorer

For simplicity reasons, I only provide a screenshot of the main program and the corresponding assembler instructions.

The Compiler Explorer allows you to visualize this compile-time calculation.

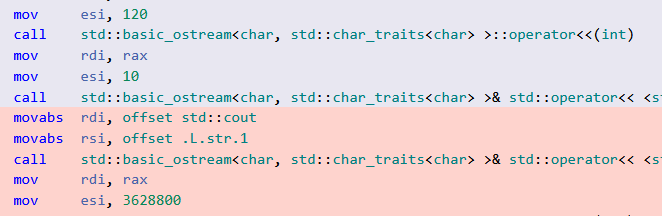
The output shows it. The factorials of 5 and 10 are just constants and were calculated during compile time. You can see the result directly in the first line and last line of the assembler instructions.

CppCon 2021

I was quite happy this week that I could use a previous post as a starting point for this post. I gave this week four talks at the CppCon and honestly, this was too much. Here are my talks that are published on Youtube’s CppCon channel. The pdfs are already available.

What’s next?

In my next post, I will continue my journey with template metaprogramming and provide more insights.

Post Views: 16,243

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS