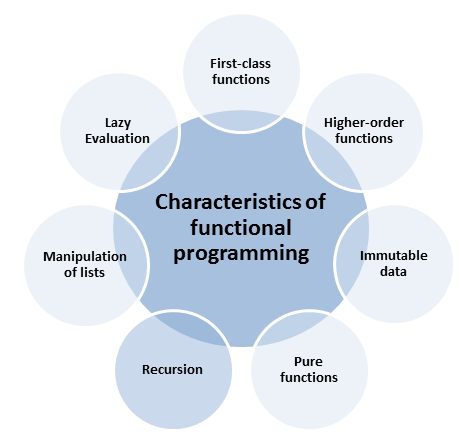
Recursion, List Manipulation, and Lazy Evaluation

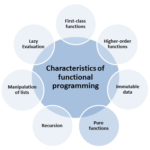
The remaining three characteristics of functional programming are told quite quickly: Recursion, manipulation of lists, and lazy e Ihop valuation.

Recursion

Pure functional languages support no mutable data. Instead of a loop, they use recursion. The meta-function from Pure Functions showed it already. At compile time, I use recursion instead of loops. The factorial function in C++

template <int N>
struct Fac{
  static int const value= N * Fac<N-1>::value;
};

template <>
struct Fac<0>{
  static int const value = 1;
};

can be written quite easily in Haskell:

Manipulation of lists

LISt Processing (LISP) is a characteristic of functional programming languages. The list is the foundation of the potent function composition in a functional language because it is the general data structure.

The processing of lists follows a simple pattern:

1. Process the first element of the list.
2. Recursively process the rest of the list, reducing each iteration by the first element.

Because list processing is so idiomatic in functional programming, there exist special names for the first element and the rest of the list: (x, xs), (head, tail), or (car, cdr).

The pattern for processing the list is directly applicable in Haskell and C++.

Firstly, the concise version of C++. The function mySum sums up the numbers from 1 to 5.

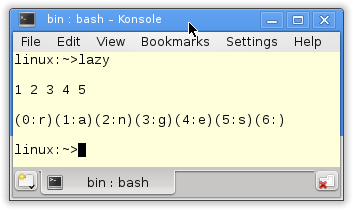
mySum []     = 0
mySum (x:xs) = x + mySum xs
mySum [1,2,3,4,5]  -- 15

And here is the C++ version.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

template<int ...> 
struct mySum;

template<>
struct mySum<>{
  static const int value= 0;
};

template<int head, int ... tail>
struct mySum<head,tail...>{
  static const int value= head + mySum<tail...>::value;
};

int sum= mySum<1,2,3,4,5>::value;  // 15

The Haskell version is relatively easy to get. Or? But the C++ version is quite heavyweight. The C++ syntax requires that the primary, also called the general template, must be declared. Line 4 to line 7 is the fully specialized template (meta-metafunction) used for the empty argument list. If at least one template argument is used, the partially specialized class template (lines 9 – 12) kicks in. Let me say a few words to the three dots, the so-called ellipse. That is why the class in line 14 can take an arbitrary number of arguments. The three dots in lines 1 and 9 pack the template parameter pack; the three dots in lines 10 and 11 unpack the function parameter pack.

Haskell and C++ apply pattern matching to use the right function.

Pattern matching

There is a subtle difference between Haskell and C++. Haskell’s matching strategy is the first match. That’s the reason you have to define the particular case first. C++ matching strategy is the best to match. You can use pattern matching to define the multiplication of two numbers by successively applying addition.

For the sake of elegance, C++ first.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

mult n 0 = 0
mult n 1 = n
mult n m = (mult n (m - 1)) + n



mult 3 2 = (mult 3 (2 - 1)) + 3
         = (mult 3 1 ) + 3
         = 3 + 3
         = 6

Lines 7 – 10 show the enrolled multiplication of the two numbers, 3 and 2. Line 1 is applied if m == 0 holds. If m == 1 holds, line 2 is used. The general case is line 3.

C++ applies a similar strategy. The difference is that the C++ version is more verbose, and I must first define the general case.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

template <int N, int M>
struct Mult{
static const int value= Mult<N, M-1>::value + N;
};
template <int N>
struct Mult<N, 1> {
static const int value= N;
};

template <int N>
struct Mult<N, 0> {
static const int value= 0;
};

std::cout << Mult<3, 2>::value << std::endl;    // 6

Lazy evaluation

The story about lazy evaluation in C++ is relatively short. That will change in C++20 with the ranges library from Eric Niebler. Lazy evaluation is the default in Haskell. Lazy evaluation means that an expression is only evaluated when needed. This strategy has two benefits.

1. Lazy evaluation helps you to save time and memory.
2. You can define algorithms on infinite data structures. Of course, you can only ask for a finite number of values at run time.

The following code snippet shows three impressive examples in Haskell:

1
2
3
4
5
6
7
8

length [2+1, 3*2, 1/0, 5-4]  -- 4

successor i= i: (successor (i+1))
take 5 ( successor 1 )     -- [1,2,3,4,5]

odds= takeWhile (< 1000) . filter odd . map (^2)
[1..]= [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 ... Control-C  
odds [1..]                 -- [1,9,25, ... , 841,961]  

I can calculate the length of a list in the first line, including the argument 1/0.  successor in line 3 defines an infinite sequence of integers. But I only request five (take 5) in line 4. Therefore, all is fine. If I want to have all integers, such as in line 7, I must hit Control-C to stop the recursion.  I can use the same expression  [1..] as an argument for the function odds. Line 6 shows the power off function composition in Haskell. The dot (.) is the symbol for function composition. With a bit of exercise, you can read the function composition in line 6 from right to left: Apply to each argument the square function; let the odd elements pass and continue as long as the resulting numbers are smaller than 1000. You can see the result of the application in the last list.

C++ uses, by default, eager evaluation. This means that contrary to Haskell, expressions are evaluated from the inside to the outside. C++ has short circuit evaluation. So, C++ is a little bit lazy. If the result of a logical expression is given before the whole expression is evaluated, C++ stops to evaluate the expression. Therefore, the following code snippet is valid in C++, although 1/0 is not defined.

if ( true or (1/0) ) std::cout << "short circuit evaluation" << std::endl;

What’s next?

With the next post, I step into the future of C++. Fold expressions in C++17 are based on variadic templates and can be used to apply the fold algorithm at compile time.

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS

Modernes C++ GmbH

Modernes C++ Mentoring (English)

"Fundamentals for C++ Professionals": open
"Design Patterns and Architectural Patterns in C++": open
"C++20: Get the Details": open
"Concurrency with Modern C++": open
"Generic Programming (Templates) with C++": October 2024
"Embedded Programming with Modern C++": October 2024
"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed about my mentoring programs? Subscribe Here

Rainer Grimm
Yalovastraße 20
72108 Rottenburg

Mobil: +49 176 5506 5086
Mail: schulung@ModernesCpp.de
Mentoring: www.ModernesCpp.org

Modernes C++ Mentoring,