More and More Save

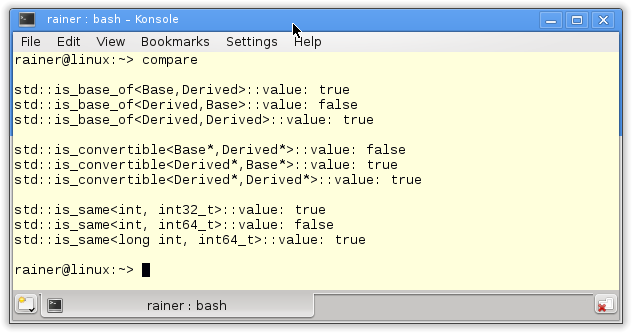
In the post Statically checked I wrote that the functions of the type-traits library are an ideal fit for static_assert. The reason is that static_assert requires a constant expression. The functions of the type-traits library provide a lot of checks which can be performed at compile time. With these posts, I will prove my statement.

gcd – The first

Before I describe systematically the functionality of the type-traits library I will start in this post with an example. My starting point is the Euclid algorithm to calculate the greatest common divisor of two numbers.

It’s quite easy to implement the algorithm as a function template and feed it with various arguments.

// gcd.cpp

#include <iostream>

template<typename T>
T gcd(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

int main(){

  std::cout << std::endl;

  std::cout << "gcd(100,10)= " <<  gcd(100,10)  << std::endl;
  std::cout << "gcd(100,33)= " << gcd(100,33) << std::endl;
  std::cout << "gcd(100,0)= " << gcd(100,0)  << std::endl;

  std::cout << gcd(3.5,4.0)<< std::endl;
  std::cout << gcd("100","10") << std::endl;

  std::cout << gcd(100,10L) << gcd(100,10L) << std::endl;

  std::cout << std::endl;

}

But the compilation of the program fails. The compiler tries in vain to instantiate the templates.

Modernes C++ Mentoring

"Fundamentals for C++ Professionals" (open)

"Design Patterns and Architectural Patterns with C++" (open)

"C++20: Get the Details" (open)

"Concurrency with Modern C++" (open)

"Generic Programming (Templates) with C++": October 2024

"Embedded Programming with Modern C++": October 2024

"Clean Code: Best Practices for Modern C++": March 2025

Do you want to stay informed: Subscribe.

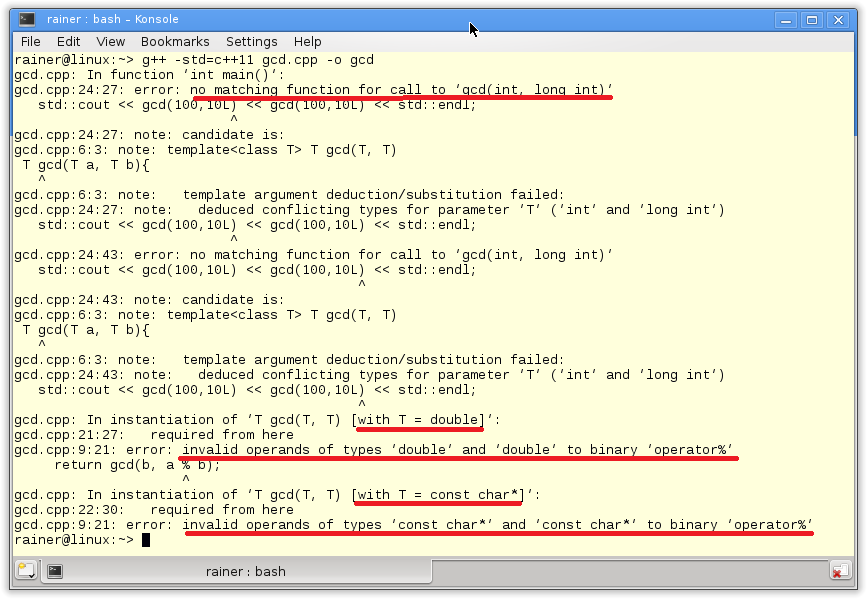
The function template has two serious issues. First, it is too generic. So the function template accepts doubles (line 21) and C strings (line 22). But it makes no sense to determine the greatest common divisor of both data types. The modulo operation for the double and the C string values fails in line 9. But that’s not the only issue. Second, gcd depend on one type parameter T. This shows the function template signature gcd(T a, T b)). a and b have to be of the same type T. There is no conversion for type parameters. Therefore, the instantiation of gcd with an int type and a long type (line 24) fails.

Thanks to the type-traits library the first issue is quickly solved. The second issue requires much more effort.

gcd – The second

I ignore for simplicity reasons in the rest of the post that both arguments have to be positive numbers. But back to the first issue. The static_assert operator and the predicate std::is_integral<T>::value helps me to check at compile time whether T is an integral type. A predicate always returns a boolean value.

// gcd_2.cpp

#include <iostream>
#include <type_traits>

template<typename T>
T gcd(T a, T b){
  static_assert(std::is_integral<T>::value, "T should be an integral type!");
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

int main(){

  std::cout << std::endl;

  std::cout << gcd(3.5,4.0)<< std::endl;
  std::cout << gcd("100","10") << std::endl;

  std::cout << std::endl;

}

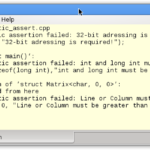
Great. I have solved the first issue of the gcd algorithm. The compilation will not fail by accident because the modulo operator is not defined for a double value and a C string. The compilation fails because the assertion in line 8 will not hold true. The subtle difference is that I now get an exact error message and not a cryptic output of a failed template instantiation as in the first example.

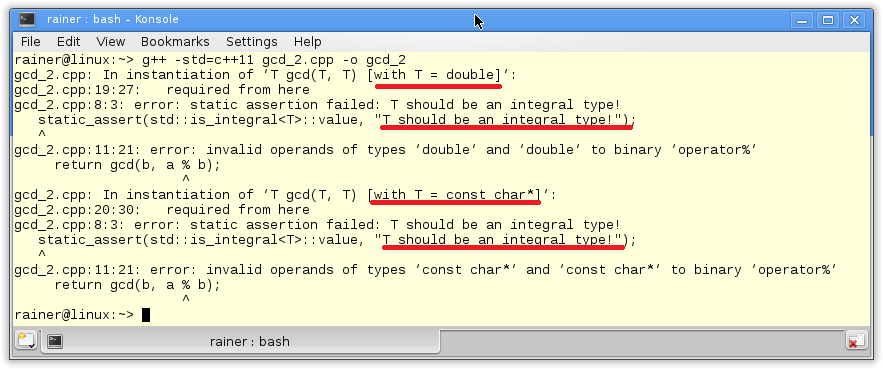
The rule is quite simple. A compilation has to fail and I should get an unambiguous error message.

But what’s about the second issue. The gcd algorithm should accept arguments of a different type.

gcd – The third

That no big deal. But stop. What is the type of the result?

template<typename T1, typename T2>
??? gcd(T1 a, T2 b){
  static_assert(std::is_integral<T1>::value, "T1 should be an integral type!");
  static_assert(std::is_integral<T2>::value, "T2 should be an integral type!");
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

The three questions marks in line 2 show the core of the issue. Should the first type or the second type be the return type of the algorithm? Or should the algorithm derive a new type from the two arguments? The type-traits library comes to my rescue. I will present two variations.

The smaller type

A good choice for the return type is to use the smaller of both types. Therefore, I need a ternary operator at compile time. Thanks to the type-traits library we have. The ternary function std::conditional operates on types and not on values. That’s because we apply the function at compile time. So we have to feed std::conditional with the right constant expression and we are done. std::conditional<(sizeof(T1) < sizeof(T2)), T1, T2>::type will return at compile time T1 if T1 is smaller than T2; it will return T2 if T1 is not smaller than T1.

Let’s apply the logic.

// gcd_3_smaller.cpp

#include <iostream>
#include <type_traits>
#include <typeinfo>

template<typename T1, typename T2>
typename std::conditional <(sizeof(T1) < sizeof(T2)), T1, T2>::type gcd(T1 a, T2 b){
  static_assert(std::is_integral<T1>::value, "T1 should be an integral type!");
  static_assert(std::is_integral<T2>::value, "T2 should be an integral type!");
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

int main(){

  std::cout << std::endl;

  std::cout << "gcd(100,10)= " <<  gcd(100,10)  << std::endl;
  std::cout << "gcd(100,33)= " << gcd(100,33) << std::endl;
  std::cout << "gcd(100,0)= " << gcd(100,0)  << std::endl;

  std::cout << std::endl;

  std::cout << "gcd(100,10LL)= " << gcd(100,10LL) << std::endl;

  std::conditional <(sizeof(100) < sizeof(10LL)), long long, long>::type uglyRes= gcd(100,10LL);
  auto res= gcd(100,10LL);
  auto res2= gcd(100LL,10L);

  std::cout << "typeid(gcd(100,10LL)).name(): " << typeid(res).name() << std::endl;
  std::cout << "typeid(gcd(100LL,10L)).name(): " << typeid(res2).name() << std::endl;

  std::cout << std::endl;

}

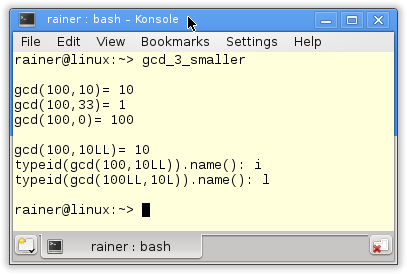
The key line of the program is the line 8 with the return type of the gcd algorithm. Of course, the algorithm can also deal with templates arguments of the same type. You can observe it in line 21 to 24 and the output of the program. But what’s about line 27? I use the number 100 of type int and the number 10 of type long long int. The result for the greatest common divisor is 10. The line 29 is extremely ugly. I have to repeat the expression std::conditional <(sizeof(100) < sizeof(10LL)), long long, long>::type to determine the right type of the variable uglyRes. Automatic type deduction with auto comes to my rescue (line 30 and 31). The typeid operator in line 33 and 34 shows that the result type of the arguments of type int and long long int is int; that the result type of the types long long int and long int is long int.

The common type

Now to my second variation. Often it is not necessary to determine the smaller type at compile time but to determine that type to which all types can implicitly be converted to. That’s the job of the function template std::common_type from the – of course you know it already – type-traits library. std::common_type can handle an arbitrary number of template arguments. To say it more formally. std::common_type is a variadic template.

// gcd_3_common.cpp

#include <iostream>
#include <type_traits>
#include <typeinfo>

template<typename T1, typename T2>
typename std::common_type<T1, T2>::type gcd(T1 a, T2 b){
  static_assert(std::is_integral<T1>::value, "T1 should be an integral type!");
  static_assert(std::is_integral<T2>::value, "T2 should be an integral type!");
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

int main(){

  std::cout << std::endl;

  std::cout << "typeid(gcd(100,10)).name(): " << typeid(gcd(100,10)).name() << std::endl;
  std::cout << "typeid(gcd(100,10L)).name(): " << typeid(gcd(100,10L)).name() << std::endl;
  std::cout << "typeid(gcd(100,10LL)).name(): " << typeid(gcd(100,10LL)).name() << std::endl;

  std::cout << std::endl;

}

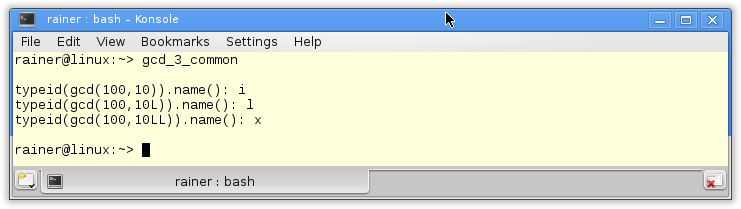
The only difference to the last implementation is that std::common_type in line 8 determines the return type. I ignore in this example the results of the gcd because I’m more interested in the types of the results. With the argument types int and int int I get int; with the argument types int and long int long int; with int and long long int long long int.

gcd – The fourth

But that’s not all. std::enable_if from the type-traits library also provides a very interesting variation. The previous implementations have in common that they will check in the function body If the arguments are integral types. The key observation is that the compiler always tries to instantiate the function temples and fails sometimes. You know the result. If the expression std::integral returns fall, the instantiation will fail. That is not the best way. It would be better if the function template is only available for the valid types. Therefore, I put the check of the function template from the template body to the template signature.

I order to concentrate on the essentials, I used the same type for the function arguments. Therefore, the return type is obvious.

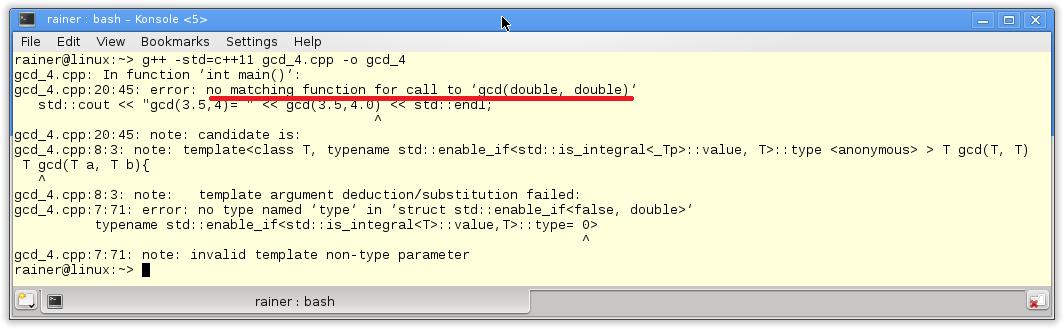
// gcd_4.cpp

#include <iostream>
#include <type_traits>

template<typename T,
         typename std::enable_if<std::is_integral<T>::value,T>::type= 0>       
T gcd(T a, T b){
  if( b == 0 ){ return a; }
  else{
    return gcd(b, a % b);
  }
}

int main(){

  std::cout << std::endl;

  std::cout << "gcd(100,10)= " <<  gcd(100,10)  << std::endl;
  std::cout << "gcd(3.5,4)= " << gcd(3.5,4.0) << std::endl;     

  std::cout << std::endl;

}

Line 7 is the critical line of the new program. The expression std::is_integral determines whether the type parameter T is integral. If T is not integral and, therefore, the return value false, I will not get a template instantiation. This is the decisive observation.

If std::enable_if returns true as the first parameter, std::enable_if will have a public member typedef type. This type is used in line 7. If std::enable_if returns false as the first parameter, std::enable_if will have no public member typedef type. Therefore line 7 is not valid. But this is not an error. Only the template for precisely this type will not be instantiated.

The rule in C++ says: When substituting the deduced type for the template parameter fails, the specialization is discarded from the overload set instead of causing a compile error. There is a shorter acronym for this rule SFINAE (Substitution Failure Is Not An Error).

The output of the compilation shows it. There is no template specialization for the type double.

What’s next?

The next post about the type-traits library will be systematic. The type-traits library has a lot of functions. They enable you to check, compare, and modify types at compile time. I will answer the two questions in the next post. How does it work? And. Which functions are available?

Post Views: 5,791

Thanks a lot to my Patreon Supporters: Matt Braun, Roman Postanciuc, Tobias Zindl, G Prvulovic, Reinhold Dröge, Abernitzke, Frank Grimm, Sakib, Broeserl, António Pina, Sergey Agafyin, Андрей Бурмистров, Jake, GS, Lawton Shoemake, Jozo Leko, John Breland, Venkat Nandam, Jose Francisco, Douglas Tinkham, Kuchlong Kuchlong, Robert Blanch, Truels Wissneth, Mario Luoni, Friedrich Huber, lennonli, Pramod Tikare Muralidhara, Peter Ware, Daniel Hufschläger, Alessandro Pezzato, Bob Perry, Satish Vangipuram, Andi Ireland, Richard Ohnemus, Michael Dunsky, Leo Goodstadt, John Wiederhirn, Yacob Cohen-Arazi, Florian Tischler, Robin Furness, Michael Young, Holger Detering, Bernd Mühlhaus, Stephen Kelley, Kyle Dean, Tusar Palauri, Juan Dent, George Liao, Daniel Ceperley, Jon T Hess, Stephen Totten, Wolfgang Fütterer, Matthias Grün, Phillip Diekmann, Ben Atakora, Ann Shatoff, Rob North, Bhavith C Achar, Marco Parri Empoli, Philipp Lenk, Charles-Jianye Chen, Keith Jeffery, Matt Godbolt, and Honey Sukesan.

Thanks, in particular, to Jon Hess, Lakshman, Christian Wittenhorst, Sherhy Pyton, Dendi Suhubdy, Sudhakar Belagurusamy, Richard Sargeant, Rusty Fleming, John Nebel, Mipko, Alicja Kaminska, Slavko Radman, and David Poole.

My special thanks to Embarcadero
My special thanks to PVS-Studio
My special thanks to Tipi.build
My special thanks to Take Up Code
My special thanks to SHAVEDYAKS